题目内容
12.如图是某算法的程序框图,若程序运行后输出的结果是27,则判断框①处应填入的条件是( )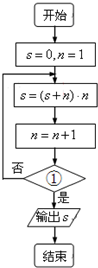
| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由框图的顺序,S=0,n=1,S=(S+n)n=(0+1)×1=1;
n=2,依次循环S=(1+2)×2=6,n=3;
n=3,依次循环S=(6+3)×3=27,n=4,
此刻输出S=27.
故判断框①处应填入的条件是n>3,
故选B.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.大量统计数据表明,某班一周内(周一到周五)各天语文、数学、外语三科有作业的概率如下表:
根据上表:
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
3.设x,y满足不等式组$\left\{{\begin{array}{l}{x+y-6≤0}\\{2x-y-1≤0}\\{3x-y-2≥0}\end{array}}\right.$,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
20.执行如图所示的程序框图,若输出S=15,则框图中①处可以填入 ( )
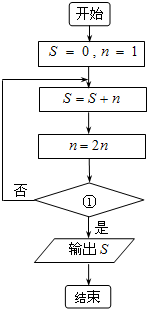

| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
7.若复数z满足(4-3i)z=|3+4i|,则z的虚部为( )
| A. | $\frac{3}{5}$i | B. | $\frac{3}{5}$ | C. | 3 | D. | 3i |
17.等差数列{an}中,若a4+a8=-3,则a6(a2+2a6+a10)的值是( )
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |
1.已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1e2的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |