题目内容
16.已知函数f(x)=$\frac{1}{x-1}$-lnx,函数y=f(|x|)的零点个数为n,则2${\;}^{lo{g}_{n}2}$等于$\sqrt{2}$.分析 判断f(|x|)为偶函数,x>0时,f(x)零点的个数m与函数y=f(|x|)的零点个数为n,有2m=n,利用函数图象交点求解,关键是判断y=$\frac{1}{x-1}$与y=lnx交点的个数.
解答 解:∵函数y=f(|x|)
∴f(|x|)=f(|-x|),f(|x|)为偶函数,
∴x>0时,f(x)零点的个数m与函数y=f(|x|)的零点个数为n,
有2m=n
∵函数f(x)=$\frac{1}{x-1}$-lnx,
∴y=$\frac{1}{x-1}$与y=lnx交点的个数与函数f(x)=$\frac{1}{x-1}$-lnx的零点的个数相等,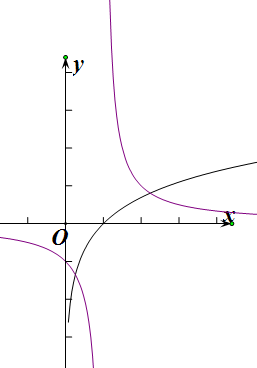
从图象可知:y=$\frac{1}{x-1}$与y=lnx交点的个数为m=2,
∴函数y=f(|x|)的零点个数为n=4,
则2${\;}^{lo{g}_{n}2}$=2${\;}^{lo{g}_{4}2}$=2${\;}^{\frac{1}{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了与一颔首图象解决函数零点,问题转化为容易化的函数图象求解,利用函数的对性简化问题,属于中档题,关键是画图象.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
7.若复数z满足(4-3i)z=|3+4i|,则z的虚部为( )
| A. | $\frac{3}{5}$i | B. | $\frac{3}{5}$ | C. | 3 | D. | 3i |
11.五个人坐成一排,甲要和乙坐在一起,乙不和丙坐在一起,则不同排法数为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
1.已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1e2的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |
6.某几何体三视图如下,图中三个等腰三角形的直角边长都是2,该几何体的体积为( )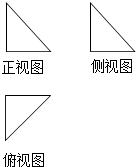

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.