ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕ‘”Ύ ΐΝ–{an}Θ§»τ¥”ΒΎΕΰœνΤπΒΡΟΩ“ΜœνΨυ¥σ”ΎΗΟœν÷°«ΑΒΡΥυ”–œνΒΡΚΆΘ§‘ρ≥Τ{an}ΈΣP ΐΝ–.
Θ®1Θ©»τ{an}ΒΡ«ΑnœνΚΆSnΘΫ3n+2Θ§ ‘≈–Εœ{an} «Ζώ «P ΐΝ–Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©…η ΐΝ–a1Θ§a2Θ§a3Θ§Γ≠Θ§a10 « ΉœνΈΣ©¹1ΓΔΙΪ≤νΈΣdΒΡΒ»≤ν ΐΝ–Θ§»τΗΟ ΐΝ– «P ΐΝ–Θ§«σdΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηΈό«ν ΐΝ–{an} « ΉœνΈΣaΓΔΙΪ±»ΈΣqΒΡΒ»±» ΐΝ–Θ§”–«ν ΐΝ–{bn}Θ§{cn} «¥”{an}÷–»Γ≥ω≤ΩΖ÷œνΑ¥‘≠ά¥ΒΡΥ≥–ρΥυΉι≥…ΒΡ≤ΜΆ§ ΐΝ–Θ§ΤδΥυ”–œνΚΆΖ÷±πΈΣT1Θ§T2Θ§«σ{an} «P ΐΝ– ±a”κqΥυ¬ζΉψΒΡΧθΦΰΘ§≤Δ÷ΛΟςΟϋΧβΓΑ»τaΘΨ0«“T1ΘΫT2Θ§‘ρ{an}≤Μ «P ΐΝ–Γ±.
ΓΨ¥πΑΗΓΩΘ®1Θ© ΐΝ–{an} «P ΐΝ–ΘΜœξΦϊΫβΈωΘ®2Θ©![]() Θ®3Θ©
Θ®3Θ©![]() Μρ
Μρ ΘΜ÷ΛΟςΦϊΫβΈω
ΘΜ÷ΛΟςΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σΫβ ΐΝ–ΒΡΆ®œνΙΪ ΫΘ§»ΜΚσΫαΚœP ΐΝ–ΒΡΧΊΒψΫχ––―ι÷ΛΘΜ
Θ®2Θ©œ»«σΫβ ΐΝ–ΒΡΆ®œνΙΪ ΫΘ§»ΜΚσΫαΚœP ΐΝ–ΒΡΧΊΒψΝ–≥ω≤ΜΒ»ΙΊœΒΘ§»ΜΚσΫχ––«σΫβΘΜ
Θ®3Θ©ΗυΨίP ΐΝ–Ϋ®ΝΔ≤ΜΒ»ΙΊœΒΘ§«σΫβ≤ΜΒ» ΫΩ…ΒΟ.
Θ®1Θ©ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Β±nΘΫ1 ±Θ§a1ΘΫS1ΘΫ5Θ§
Ι ![]() Θ§
Θ§
ѫϥ±![]() ±Θ§
±Θ§![]() Θ§ΖϊΚœΧβ“βΘ§
Θ§ΖϊΚœΧβ“βΘ§
Ι ΐΝ–{an} «P ΐΝ–.
Θ®2Θ©”…Χβ“β÷ΣΘ§ΗΟ ΐΝ–ΒΡ«ΑnœνΚΆΈΣ![]() Θ§
Θ§
”… ΐΝ–a1Θ§a2Θ§a3Θ§Γ≠Θ§a10 «P ΐΝ–Θ§Ω…÷Σa2ΘΨS1ΘΫa1Θ§Ι ΙΪ≤νdΘΨ0Θ§
![]() Ε‘¬ζΉψnΘΫ1Θ§2Θ§3Θ§
Ε‘¬ζΉψnΘΫ1Θ§2Θ§3Θ§![]() Θ§9ΒΡ»Έ“βnΕΦ≥…ΝΔΘ§‘ρ
Θ§9ΒΡ»Έ“βnΕΦ≥…ΝΔΘ§‘ρ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Ι dΒΡ»Γ÷ΒΖΕΈßΈΣ![]() .
.
Θ®3Θ©ΔΌ»τ{an} «P ΐΝ–Θ§‘ρaΘΫS1ΘΦa2ΘΫaqΘ§
»τaΘΨ0Θ§‘ρqΘΨ1Θ§”÷”…an+1ΘΨSnΕ‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§Ω…÷Σ![]() Θ§Φ¥
Θ§Φ¥![]() Ε‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§
Ε‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§
”…![]() Θ§Ι 2©¹qΓή0Θ§Ω…ΒΟqΓί2Θ§ΘΜ
Θ§Ι 2©¹qΓή0Θ§Ω…ΒΟqΓί2Θ§ΘΜ
»τaΘΦ0Θ§‘ρqΘΦ1Θ§”÷”…an+1ΘΨSnΕ‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§Ω…÷Σ![]() Θ§Φ¥Θ®2©¹qΘ©qnΘΦ1Ε‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§
Θ§Φ¥Θ®2©¹qΘ©qnΘΦ1Ε‘“Μ«–’ΐ’ϊ ΐnΕΦ≥…ΝΔΘ§
”÷Β±qΓ Θ®©¹ΓόΘ§©¹1] ±Θ§Θ®2©¹qΘ©qnΘΦ1Β±nΘΫ2 ±≤Μ≥…ΝΔΘ§
Ι ”–![]() Μρ
Μρ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
ΓύΒ±{an} «P ΐΝ– ±Θ§a”κq¬ζΉψΒΡΧθΦΰΈΣ![]() Μρ
Μρ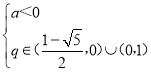 ΘΜ
ΘΜ
ΔΎΦΌ…η{an} «P ΐΝ–Θ§‘ρ”…ΔΌΩ…÷ΣΘ§qΓί2Θ§aΘΨ0Θ§«“{an}÷–ΟΩ“ΜœνΨυΈΣ’ΐ ΐΘ§
»τ{bn}÷–ΒΡΟΩ“ΜœνΕΦ‘Ύ{cn}÷–Θ§‘ρ”…’βΝΫ ΐΝ– «≤ΜΆ§ ΐΝ–Θ§Ω…÷ΣT1ΘΦT2ΘΜ
»τ{cn}÷–ΒΡΟΩ“ΜœνΕΦ‘Ύ{bn}÷–Θ§Ά§άμΩ…ΒΟT1ΘΨT2ΘΜ
»τ{bn}÷–÷Ν…Ό”–“Μœν≤Μ‘Ύ{cn}÷–«“{cn}÷–÷Ν…Ό”–“Μœν≤Μ‘Ύ{bn}÷–Θ§
…η{bn'}Θ§{cn' «ΫΪ{bn}Θ§{cn}÷–ΒΡΙΪΙ≤œν»ΞΒτ÷°ΚΆ Θ”ύœν“ά¥ΈΙΙ≥…ΒΡ ΐΝ–Θ§ΥϋΟ«ΒΡΥυ”–œνΚΆΖ÷±πΈΣT1'Θ§T2'Θ§
≤ΜΖΝ…η{bn'}Θ§{cn'}÷–Ήν¥σΒΡœν‘Ύ{bn'}÷–Θ§…ηΈΣamΘ®mΓί2Θ©Θ§
‘ρT2'Γήa1+a2+Γ≠Γ≠+am©¹1ΘΦamΓήT1'Θ§Ι T2'ΘΦT1'Θ§Ι Ήή”–T1ΓΌT2”κT1ΘΫT2Ο§ΕήΘ§Ι ΦΌ…η¥μΈσΘ§‘≠ΟϋΧβ’ΐ»Ζ.

