题目内容
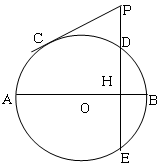
如图,直径AB=2,C是圆O上的一点,连接BC并延长至D, 使|CD|=|BC|,若AC与OD的交点P,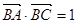 ,则
,则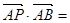
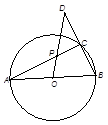
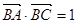 ,则
,则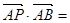
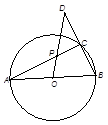
2
试题分析:由于直径所对的圆周角为直角,同时|CD|=|BC|,延长CO到与圆相交于点E,则三角形BEC,和三角形BAC全等,同时要根据
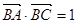 ,得到BC的长度为1,同时得到
,得到BC的长度为1,同时得到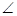 ABC=
ABC=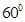 ,那么对于
,那么对于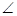 CAB=
CAB=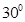 ,然后结合三角形APO,相似于三角形DCP,进而得到关系式AP:PC=OP:PD,然后根据已知中的向量的数量积公式得到
,然后结合三角形APO,相似于三角形DCP,进而得到关系式AP:PC=OP:PD,然后根据已知中的向量的数量积公式得到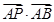 的值为2,故填写答案为2
的值为2,故填写答案为2点评:对于几何求解中直线与圆,以及三角形与圆的性质的综合运用,是高考的一个考向,值得关注,同时对于适当的作出辅助线是解题的难点,需要多加训练,属于中档题。

练习册系列答案
相关题目
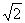 ,
,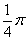 ),曲线C的参数方程为
),曲线C的参数方程为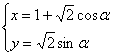 (
(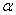 为参数),则点M到曲线C上的点的距离的最小值为 .
为参数),则点M到曲线C上的点的距离的最小值为 .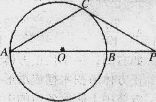
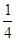 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 
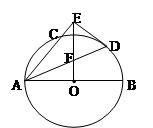
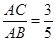 ,求
,求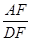 的值.
的值.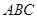 中,∠
中,∠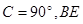 是角平分线,
是角平分线,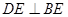 交
交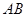 于
于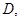 ⊙
⊙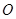 是△
是△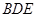 的外接圆。
的外接圆。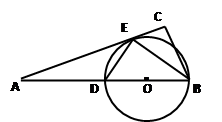
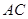 是⊙
是⊙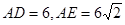 ,求
,求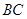 的长。
的长。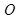 的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为
的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为 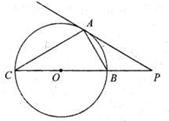
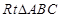 中,
中,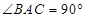 ,
,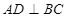 ,
,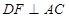 ,垂足为F,
,垂足为F,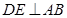 ,垂足为E.
,垂足为E.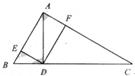
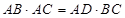 ;
;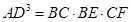
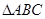 中,
中,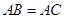 ,
,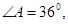 D在AB上,
D在AB上,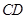 是
是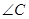 的平分线,则
的平分线,则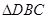 的面积与
的面积与
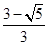
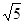 ,求PD的长.
,求PD的长.