题目内容
如上图,弧BE是半径为 6 的⊙D的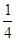 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 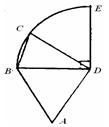
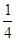 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 
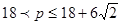
试题分析:根据题意,由于弧BE是半径为 6 的⊙D的
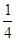 圆周,那么可知AD=AB=BD=6,DC=6,而△ABD是等边三角形,则可知,C点是弧BE上的任意一点,那么可知四边形ABCD的周长p的取值范围
圆周,那么可知AD=AB=BD=6,DC=6,而△ABD是等边三角形,则可知,C点是弧BE上的任意一点,那么可知四边形ABCD的周长p的取值范围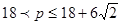 ,故答案为
,故答案为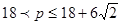 。
。点评:解决的关键是是表示四边形的周长,利用之就爱哦三就爱哦行以及弧的半径和正三角形的知识得到结论。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
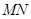 交圆
交圆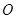 于
于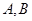 两点,
两点,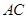 是直径,
是直径,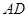 平分
平分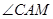 ,交圆
,交圆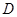 , 过
, 过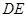 丄
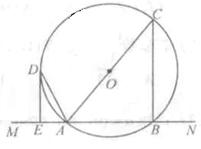
丄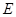 .
.
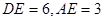 ,求
,求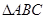 的面积
的面积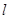 ,过A作直线
,过A作直线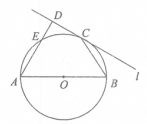
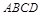 中,
中,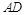 ∥BC,点
∥BC,点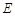 ,
,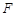 分别在边
分别在边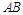 ,
,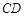 上,设
上,设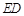 与
与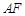 相交于点
相交于点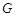 ,若
,若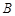 ,
,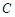 ,
,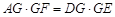 .
. 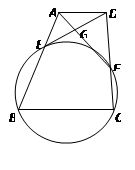
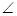 AMB=30o,那么⊙O2的半径为 ;
AMB=30o,那么⊙O2的半径为 ;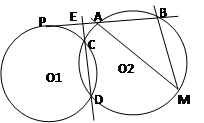
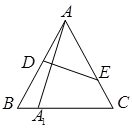
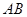 是
是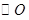 的直径,
的直径,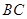 是
是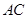 与
与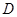 ,若
,若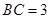 ,
,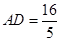 ,则
,则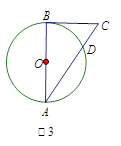
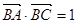 ,则
,则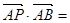
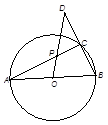
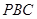 经过圆心O,
经过圆心O,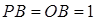 , OP绕点
, OP绕点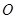 逆时针旋120°到
逆时针旋120°到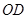 ,连
,连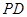 交圆
交圆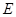 ,则
,则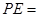 .
.