题目内容
在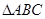 中,
中,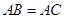 ,
,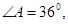 D在AB上,
D在AB上,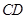 是
是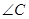 的平分线,则
的平分线,则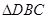 的面积与
的面积与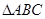 的面积之比是:
的面积之比是:
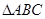 中,
中,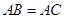 ,
,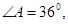 D在AB上,
D在AB上,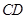 是
是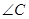 的平分线,则
的平分线,则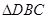 的面积与
的面积与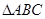 的面积之比是:
的面积之比是: A.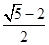 | B.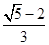 | C.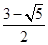 | D.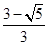 |
C
根据等腰三角形的两个底角相等和三角形的内角和定理,可以求得∠ABC=∠ACB=72°,根据角平分线定义,可得∠BCD=∠ACD=36°;根据两角对应相等,得△DBC∽△BCA,设AB=x,BC=y,根据等腰三角形的性质,则AD=CD=BC=y,则BD=x-y.根据相似三角形的性质求得y:x的值即可.设AB=x,BC=y.
∵△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.∵CD是角平分线,∴∠BCD=∠ACD=36°.∴

AD=CD=BC=y,
∴BD=x-y.∵∠BCD=∠A=36°,∠B=∠ACB=72°,∴△DBC∽△ABC,然后可知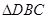 的面积与
的面积与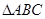 的面积之比为
的面积之比为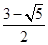 ,选C.
,选C.
∵△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.∵CD是角平分线,∴∠BCD=∠ACD=36°.∴

AD=CD=BC=y,
∴BD=x-y.∵∠BCD=∠A=36°,∠B=∠ACB=72°,∴△DBC∽△ABC,然后可知
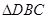 的面积与
的面积与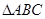 的面积之比为
的面积之比为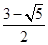 ,选C.
,选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
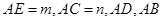 为方程
为方程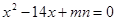 的两根,
的两根,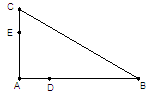
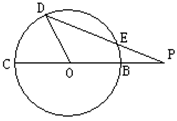
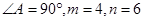 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。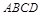 中,
中,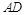 ∥BC,点
∥BC,点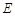 ,
,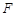 分别在边
分别在边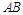 ,
,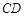 上,设
上,设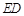 与
与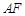 相交于点
相交于点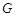 ,若
,若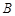 ,
,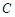 ,
,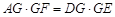 .
. 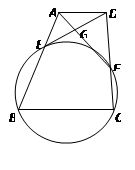
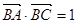 ,则
,则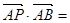
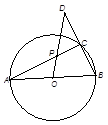
 的⊙
的⊙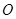 中,
中,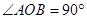 ,
,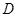 为
为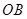 的中点,
的中点,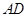 的延长线交⊙
的延长线交⊙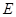 ,则线段
,则线段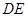 的长为 .
的长为 .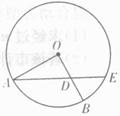
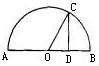
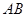 是半圆
是半圆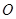 的直径,点
的直径,点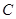 在半圆上,
在半圆上,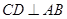 于
于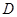 ,且
,且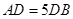 ,设
,设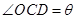 ,则
,则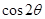 =________。
=________。 
 是圆
是圆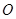 外的一点,
外的一点,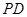 为切线,
为切线,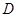 为切点,割线
为切点,割线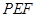 经过圆心
经过圆心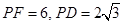 ,则
,则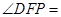 __ ___.
__ ___.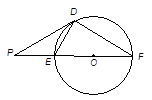
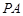 是圆
是圆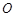 的切线,
的切线,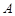 是切点,直线
是切点,直线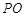 交圆
交圆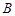 、
、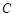 两点,
两点,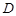 是
是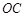 的中点,连结
的中点,连结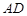 并延长交圆
并延长交圆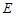 ,若
,若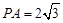 ,∠
,∠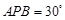 ,则
,则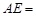 ________.
________.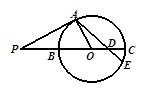
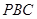 经过圆心O,
经过圆心O,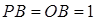 , OP绕点
, OP绕点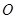 逆时针旋120°到
逆时针旋120°到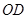 ,连
,连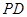 交圆
交圆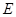 ,则
,则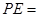 .
.