题目内容
(本小题满分10分)
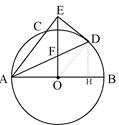
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
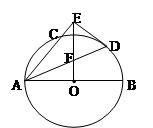
(1)求证:DE是⊙O的切线;
(2)若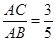 ,求
,求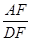 的值.
的值.
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.

(1)求证:DE是⊙O的切线;
(2)若
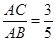 ,求
,求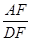 的值.
的值.(1)结合同弧所对的圆周角相等来求解直线DE⊥OD,同时OD是圆的半径来说明是切线
(2)根据题意可知△AED∽△ADB可得 AD2=AC·AB
求解得到AE,又由△AEF∽△DOF,得到比值。
(2)根据题意可知△AED∽△ADB可得 AD2=AC·AB
求解得到AE,又由△AEF∽△DOF,得到比值。
试题分析:略证 (1) 连结OD,可得∠ODA=∠OAD=∠DAC ……2分
∴OD∥AE 又AE⊥DE …………3分
∴DE⊥OD,又OD为半径 ∴ DE是的⊙O切线 …………5分
⑵ 提示:过D作DH⊥AB于H 则有∠DOH=∠CAB
Cos∠DOH=cos∠CAB=
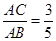 ……………………6分
……………………6分设OD=5x,则AB=10x,OH=3x,DH=4x
∴AH=8x AD2=80x2
由△AED∽△ADB可得 AD2=AC·AB=AC·10x
∴AE=8X…………8分
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =
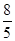 ;
;∴
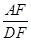 =
=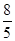 ……10分
……10分点评:解决该试题的关键是利用垂直关系证明相切同时利用相似比来求解比值问题,属于基础题。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
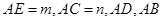 为方程
为方程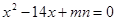 的两根,
的两根,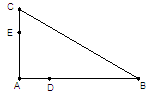
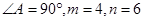 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。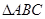 中,
中,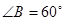 ,
,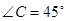 ,高
,高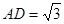 ,在
,在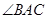 内作射线
内作射线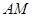 交
交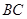 于点
于点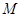 ,则
,则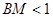 的概率为( )
的概率为( )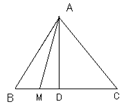
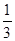
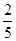
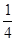
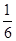
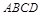 中,
中,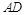 ∥BC,点
∥BC,点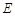 ,
,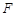 分别在边
分别在边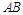 ,
,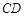 上,设
上,设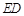 与
与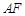 相交于点
相交于点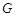 ,若
,若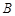 ,
,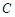 ,
,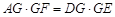 .
. 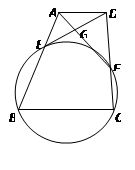
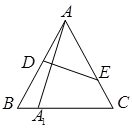
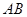 是
是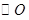 的直径,
的直径,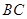 是
是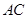 与
与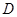 ,若
,若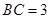 ,
,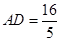 ,则
,则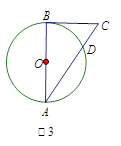
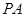 与圆
与圆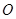 相切于点
相切于点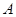 ,经过点
,经过点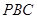 交圆
交圆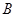 、
、 ,
,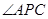 的平分线分别交
的平分线分别交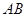 、
、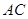 于点
于点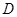 、
、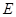 .
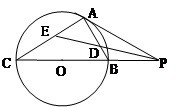
.
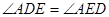 .
.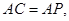 求
求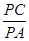 的值.
的值.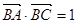 ,则
,则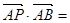
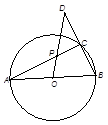
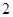 的⊙
的⊙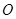 中,
中,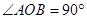 ,
,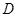 为
为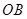 的中点,
的中点,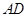 的延长线交⊙
的延长线交⊙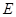 ,则线段
,则线段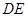 的长为 .
的长为 .