题目内容
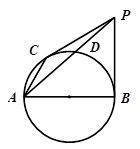
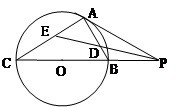
如图:PA为圆 的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为
的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为 
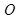 的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为
的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为 

试题分析:连接AB,根据切割线定理有,
PA2=PB•PC,
∴102=5×(5+BC),解得BC=15,
又∵∠PAB=∠PCA,∠APB=∠CPA,∴△APB∽△CPA,
∴PA:AB=PC:AC,
∴10:AB=20:AC①;
∵BC是直径,
∴AB2+AC2=BC2,
∴AB2+AC2=152②;
①②联立解得AC=
 ,故选D。
,故选D。点评:简单题,平面几何作为选考内容,往往难度不大,注意分析图形特征,特别是分析构造直角三角形。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 是圆内接四边形,延长
是圆内接四边形,延长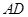 与的延长线
与的延长线 交于点
交于点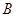 ,且
,且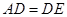 ,
, 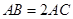 .
.
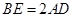 ;
;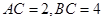 时,求
时,求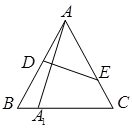
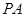 与圆
与圆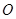 相切于点
相切于点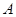 ,经过点
,经过点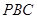 交圆
交圆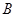 、
、 ,
,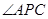 的平分线分别交
的平分线分别交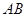 、
、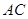 于点
于点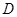 、
、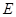 .
.
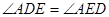 .
.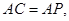 求
求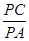 的值.
的值.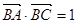 ,则
,则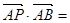
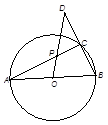
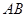 是⊙
是⊙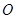 的一条弦,点
的一条弦,点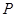 为
为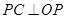 ,
,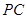 交⊙
交⊙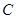 ,若
,若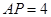 ,
,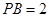 ,则
,则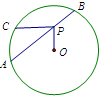
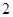 的⊙
的⊙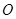 中,
中,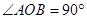 ,
, 为
为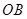 的中点,
的中点,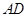 的延长线交⊙
的延长线交⊙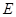 ,则线段
,则线段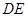 的长为 .
的长为 .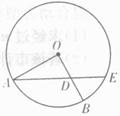
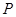 是圆
是圆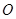 外的一点,
外的一点,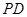 为切线,
为切线,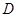 为切点,割线
为切点,割线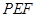 经过圆心
经过圆心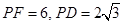 ,则
,则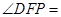 __ ___.
__ ___.