题目内容
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
月收入(百元) | 赞成人数 |
[15,25) | 8 |
[25,35) | 7 |
[35,45) | 10 |
[45,55) | 6 |
[55,65) | 2 |
[65,75) | 2 |
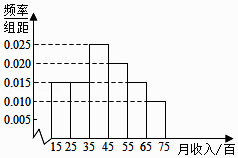
(Ⅰ)试根据频率分布直方图估计这60人的中位数和平均月收入;
(Ⅱ)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求被选取的2人都不赞成的概率.
【答案】解:(Ⅰ)设中位数为x,由直方图知: 10×0.015+10×0.015+(x﹣35)×0.025=0.5,
解得x=43;
平均数为 ![]() =(20×0.015+30×0.015+40×0.025+50×0.02+60×0.015+70×0.01)×10=43.5;
=(20×0.015+30×0.015+40×0.025+50×0.02+60×0.015+70×0.01)×10=43.5;
∴这60人的平均月收入约为43.5百元;
(Ⅱ)月收入为(单位:百元)在[65,75)的人数为:
60×10×0.01=6人,
由表格赞成人数2人,则不赞成的4人为:
记不赞成的人为:a,b,c,d;赞成人数为:A,B
则从这6人中随机地选取2人一共有15种结果如下:
ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB;
其中被选取的2人都不赞成的结果有6种结果如下:
ab,ac,ad,bc,bd,cd;
记事件A:“被选取的2人都不赞成”,
则:P(A)= ![]() =
= ![]() =
= ![]() ;
;
故被选取的2人都不赞成的概率为 ![]() .
.
【解析】(Ⅰ)根据中位数的两边频率相等,列出方程即可求出中位数; 利用频率分布直方图中各小矩形的底边中点坐标×对应的频率,再求和,即得平均数;(Ⅱ)利用列举法求出基本事件数,计算对应的概率值.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
