题目内容
【题目】已知函数f(x)= ![]() ,若|f(x)|≥ax,则a的取值范围是( )
,若|f(x)|≥ax,则a的取值范围是( )
A.(﹣∞,0]
B.(﹣∞,1]
C.[﹣2,1]
D.[﹣2,0]
【答案】D
【解析】解:由题意可作出函数y=|f(x)|的图像,和函数y=ax的图像, 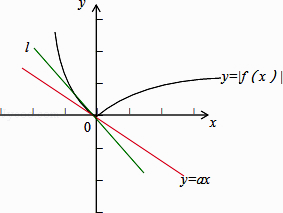
由图像可知:函数y=ax的图像为过原点的直线,当直线介于l和x轴之间符合题意,直线l为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x2﹣2x,
求其导数可得y′=2x﹣2,因为x≤0,故y′≤﹣2,故直线l的斜率为﹣2,
故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[﹣2,0]
故选:D
由函数图像的变换,结合基本初等函数的图像可作出函数y=|f(x)|的图像,和函数y=ax的图像,由导数求切线斜率可得l的斜率,进而数形结合可得a的范围.

【题目】某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示. 
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | ① | 0.350 |
第3组 | [170,175) | 30 | ② |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185) | 10 | 0.100 |
合计 | 100 | 1.00 | |
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
月收入(百元) | 赞成人数 |
[15,25) | 8 |
[25,35) | 7 |
[35,45) | 10 |
[45,55) | 6 |
[55,65) | 2 |
[65,75) | 2 |
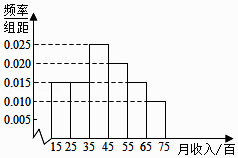
(Ⅰ)试根据频率分布直方图估计这60人的中位数和平均月收入;
(Ⅱ)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求被选取的2人都不赞成的概率.