题目内容
【题目】已知椭圆的中心在原点，焦点在x轴上，离心率为 
，且经过点M（4，1），直线l：y=x+m交椭圆于不同的两点A，B． （Ⅰ）求椭圆的方程；
（Ⅱ）求m的取值范围；
（Ⅲ）若直线l不过点M，求证：直线MA、MB与x轴围成一个等腰三角形．
【答案】解：（Ⅰ）设椭圆的方程为 
， ∵椭圆的离心率为 
，
∴a2=4b2 ，
又∵M（4，1），
∴ 
，解得b2=5，a2=20，故椭圆方程为 
．
（Ⅱ）将y=x+m代入 并整理得
5x2+8mx+4m2﹣20=0，
∵直线l：y=x+m交椭圆于不同的两点A，B
∴△=（8m）2﹣20（4m2﹣20）＞0，解得﹣5＜m＜5．
（Ⅲ）设直线MA，MB的斜率分别为k1和k2 ， 只要证明k1+k2=0．
设A（x1 ， y1），B（x2 ， y2），
根据（Ⅱ）中的方程，利用根与系数的关系得： 
．
上式的分子=（x1+m﹣1）（x2﹣4）+（x2+m﹣1）（x1﹣4）
=2x1x2+（m﹣5）（x1+x2）﹣8（m﹣1）
= 
所以k1+k2=0，得直线MA，MB的倾斜角互补
∴直线MA、MB与x轴围成一个等腰三角形
【解析】（I）设出椭圆的标准方程，根据椭圆的离心率为 
，得出a2=4b2 ， 再根据M（4，1）在椭圆上，解方程组得b2=5，a2=20，从而得出椭圆的方程；（II）因为直线l：y=x+m交椭圆于不同的两点A，B，可将直线方程与椭圆方程消去y得到关于x的方程，有两个不相等的实数根，从而△＞0，解得﹣5＜m＜5；（III）设出A（x1 ， y1），B（x2 ， y2），对（II）的方程利用根与系数的关系得： 
．再计算出直线MA的斜率k1= 
，MB的斜率为k2= 
，将式子K1+K2通分化简，最后可得其分子为0，从而得出k1+k2=0，得直线MA，MB的倾斜角互补，命题得证．
阅读快车系列答案
【题目】已知等差数列{an}的前n项和为Sn ， S3=﹣15，且a1+1，a2+1，a4+1成等比数列，公比不为1．
（1）求数列{an}的通项公式；
（2）设bn= 
，求数列{bn}的前n项和Tn ．
【题目】2016年5月20日，针对部分“二线城市”房价上涨过快，媒体认为国务院常务会议可能再次确定五条措施（简称“国五条”）．为此，记者对某城市的工薪阶层关于“国五条”态度进行了调查，随机抽取了60人，作出了他们的月收入的频率分布直方图（如图），同时得到了他们的月收入情况与“国五条”赞成人数统计表（如表）：
月收入（百元） | 赞成人数 |
[15，25） | 8 |
[25，35） | 7 |
[35，45） | 10 |
[45，55） | 6 |
[55，65） | 2 |
[65，75） | 2 |
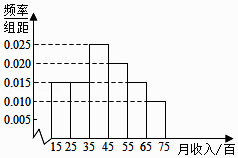
（Ⅰ）试根据频率分布直方图估计这60人的中位数和平均月收入；
（Ⅱ）若从月收入（单位：百元）在[65，75）的被调查者中随机选取2人进行追踪调查，求被选取的2人都不赞成的概率．
