题目内容
【题目】已知定义在区间[﹣ ![]() ,π]上的函数y=f(x)的图象关于直线x=
,π]上的函数y=f(x)的图象关于直线x= ![]() 对称,当x≥
对称,当x≥ ![]() 时,函数y=sinx.
时,函数y=sinx.
(1)求f(﹣ ![]() ),f(﹣
),f(﹣ ![]() )的值;
)的值;
(2)求y=f(x)的表达式
(3)若关于x的方程f(x)=a有解,那么将方程在a取某一确定值时所求得的所有解的和记为Ma , 求Ma的所有可能取值及相应a的取值范围.
【答案】
(1)解:f(﹣ ![]() )=f(π)=sinπ=0,
)=f(π)=sinπ=0,
f(﹣ ![]() )=f(
)=f( ![]() )=sin
)=sin ![]() =
= ![]()
(2)解:设﹣ ![]() ,则
,则 ![]() ,
,
∴f(x)=f( ![]() )=sin(
)=sin( ![]() )=cosx,
)=cosx,
∴f(x)= 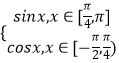
(3)解:作函数f(x)的图象如下:
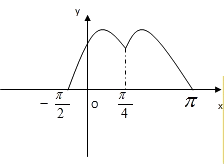
显然,若f(x)=a有解,则a∈[0,1].
① 若0 ![]() ,f(x)=a有两解,Ma=
,f(x)=a有两解,Ma= ![]() ;
;
②若a= ![]() ,f(x)=a有三解,Ma=
,f(x)=a有三解,Ma= ![]() ;
;
③若 ![]() <a<1,f(x)=a有四解,Ma=π;
<a<1,f(x)=a有四解,Ma=π;
④若a=1,f(x)=a有两解,Ma= ![]() ;
;
综上所述,当0≤a< ![]() 或a=1时,f(x)=a有两解,Ma=
或a=1时,f(x)=a有两解,Ma= ![]() ;
;
当a= ![]() 时,f(x)=a有三解,Ma=
时,f(x)=a有三解,Ma= ![]() ;
;
当 ![]() 时,f(x)=a有四解,Ma=π
时,f(x)=a有四解,Ma=π
【解析】(1)由题意可求f(﹣ ![]() )=f(π)=sinπ=0,f(﹣
)=f(π)=sinπ=0,f(﹣ ![]() )=f(
)=f( ![]() )=sin
)=sin ![]() =
= ![]() .(2)设﹣
.(2)设﹣ ![]() ,则
,则 ![]() ,由f(x)=f(
,由f(x)=f( ![]() )=sin(
)=sin( ![]() )=cosx,即可解得分段函数的解析式f(x)=
)=cosx,即可解得分段函数的解析式f(x)= 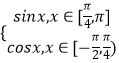 .(3)作函数f(x)的图象,若f(x)=a有解,则a∈[0,1],分情况讨论即可得解.
.(3)作函数f(x)的图象,若f(x)=a有解,则a∈[0,1],分情况讨论即可得解.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生. 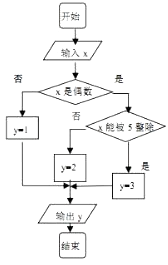
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 24 | 19 | 7 |
… | … | … | … |
2000 | 1027 | 776 | 197 |
乙的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 26 | 11 | 13 |
… | … | … | … |
2000 | 1051 | 396 | 553 |
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
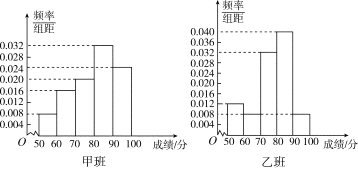
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |