题目内容
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)
【解析】试题分析:(1)由题意得曲线![]() 是以F(0,1)为焦点,以y=﹣1为准线的抛物线,进而可得其方程为
是以F(0,1)为焦点,以y=﹣1为准线的抛物线,进而可得其方程为![]() 。(2)设直线
。(2)设直线![]() 为y=kx+1,代入抛物线方程消去y可得
为y=kx+1,代入抛物线方程消去y可得![]() ,设A(x1,y1),B(x2,y2),则
,设A(x1,y1),B(x2,y2),则![]() ,由
,由![]() 得
得![]() ,又
,又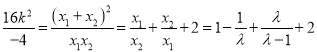 ,可构造
,可构造![]() ,由函数的单调性可得
,由函数的单调性可得![]() ,即
,即![]() ,解得
,解得![]() 。即为所求。
。即为所求。
试题解析:
(1)由题意得动点P(x,y)到F(0,1)的距离等于它到直线y=﹣1的距离,
∴ 动点P的轨迹是以F(0,1)为焦点,以y=﹣1为准线的抛物线,
设其方程为![]() ,
,
由条件得![]() .
.
∴ 曲线![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意设直线![]() 的方程为y=kx+1,
的方程为y=kx+1,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵ 直线![]() 与抛物线相交,
与抛物线相交,
∴![]() ,
,
设A(x1,y1),B(x2,y2),则![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() 可得
可得
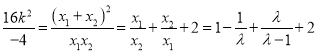 ,
,
即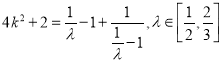 ,
,
∵![]() ,∴
,∴![]() 。
。
设![]() ,则函数
,则函数![]() 在
在![]() 上单调递减。
上单调递减。
∴![]() ,即
,即![]() 。
。
由![]() 得
得![]() ,满足
,满足![]() 。
。
∴![]() 的取值范围为
的取值范围为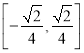 。
。

 阅读快车系列答案
阅读快车系列答案【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生. 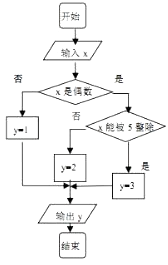
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 24 | 19 | 7 |
… | … | … | … |
2000 | 1027 | 776 | 197 |
乙的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 26 | 11 | 13 |
… | … | … | … |
2000 | 1051 | 396 | 553 |
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.