题目内容
(本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,
前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明: n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明:
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.(Ⅰ)解:因为Sn=na+n (n-1),
S1=a,S2=2a+2,S4=4a+12.由于S1,S2,S4成等比数列,因此
 =S1
=S1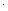 S4,即得a=1.an=2n-1.
S4,即得a=1.an=2n-1.
(Ⅱ)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即 .因此
.因此
a2+2ma+2m(m+1)=0,
要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列
S1=a,S2=2a+2,S4=4a+12.由于S1,S2,S4成等比数列,因此
 =S1
=S1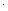 S4,即得a=1.an=2n-1.
S4,即得a=1.an=2n-1. (Ⅱ)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即
 .因此
.因此a2+2ma+2m(m+1)=0,
要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列
略

练习册系列答案
相关题目
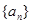 的前n项和为
的前n项和为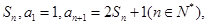 等差数列
等差数列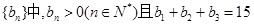 ,又
,又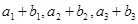 成等比数列.
成等比数列.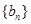 的通项公式;
的通项公式;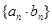 的前n项和
的前n项和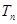 .
. 的前n项和为
的前n项和为 ,且
,且 ,(n=1,2,3…)数列
,(n=1,2,3…)数列 中,
中, ,点
,点 在直线
在直线 上。
上。 ,求满足
,求满足 的最大正整数n。
的最大正整数n。 ,数列
,数列 和
和 满足:
满足: ,
, ,函数
,函数 的图像在点
的图像在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 .
.  }的通项公式;
}的通项公式; 的项中仅
的项中仅 最小,求
最小,求 的取值范围;
的取值范围;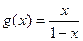 ,令函数
,令函数 数列
数列 满足:
满足: 且
且 证明:
证明: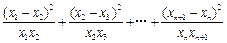
 .
.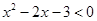 的整数解构成等差数列
的整数解构成等差数列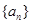 ,且
,且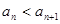 ,则数列
,则数列 的前
的前 项和
项和 和通项
和通项 满足
满足 数列
数列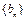 中,
中,
 满足
满足 是否存在正整数
是否存在正整数 ,使得
,使得 时
时 恒成立?若存在,求
恒成立?若存在,求 满足
满足
 ,则
,则 =_________;
=_________;
 满足
满足 ,则
,则