题目内容
(本小题满分12分)已知数列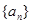 的前n项和为
的前n项和为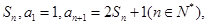 等差数列
等差数列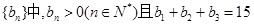 ,又
,又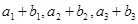 成等比数列.
成等比数列.
(I)求数列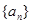 、
、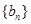 的通项公式;
的通项公式;
(II)求数列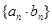 的前n项和
的前n项和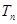 .
.
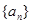 的前n项和为
的前n项和为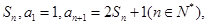 等差数列
等差数列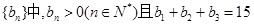 ,又
,又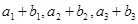 成等比数列.
成等比数列.(I)求数列
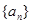 、
、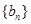 的通项公式;
的通项公式;(II)求数列
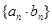 的前n项和
的前n项和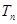 .
.解:(1) 。
。
 ,
,
 .
.
而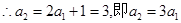 .
.
 数列
数列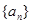 是以1为首项,3为公比的等比数列.
是以1为首项,3为公比的等比数列.
 . (4分)
. (4分)
 .
.
在等差数列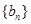 中,
中, ,
, .
.
设等数列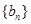 的公差为
的公差为 、
、 、
、 成等比数列,
成等比数列,
 .
.
 ,解得
,解得 或
或 ,
,
 舍去
舍去 ,取
,取 ,
,
 . (8分)
. (8分)
(3)由(1)知 ,则
,则
 ,① (9分)
,① (9分)
 ,②
,②
 ①-②,得
①-②,得
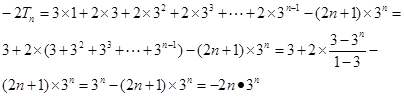
 . (12分)
. (12分)
 。
。 ,
, .
.而
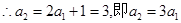 .
. 数列
数列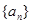 是以1为首项,3为公比的等比数列.
是以1为首项,3为公比的等比数列. . (4分)
. (4分) .
.在等差数列
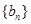 中,
中, ,
, .
.设等数列
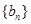 的公差为
的公差为 、
、 、
、 成等比数列,
成等比数列, .
. ,解得
,解得 或
或 ,
, 舍去
舍去 ,取
,取 ,
, . (8分)
. (8分) (3)由(1)知
 ,则
,则 ,① (9分)
,① (9分) ,②
,②  ①-②,得
①-②,得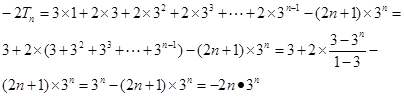
 . (12分)
. (12分)略

练习册系列答案
相关题目
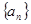 的前
的前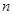 项和为
项和为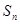 ,
,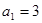 ,若数列
,若数列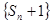 是公比为
是公比为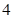 的等比数列.
的等比数列. 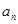 ;
;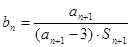 ,
,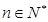 ,求数列
,求数列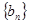 的前
的前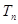 .
.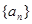 是的前n项和为Sn,满足
是的前n项和为Sn,满足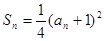
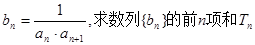
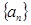 中,
中,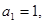 且点
且点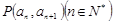 在直线
在直线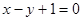 上。
上。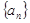 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数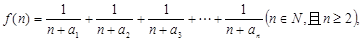 求函数
求函数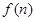 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设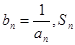 表示数列
表示数列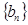 的前
的前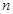 项和。试问:是否存在关于
项和。试问:是否存在关于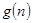 ,使得
,使得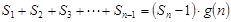 对于一切不小于2的自然数
对于一切不小于2的自然数 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.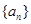 的各项均为正数,且
的各项均为正数,且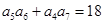 ,则
,则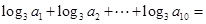 ( )
( )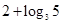
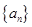 中,
中,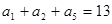 ,且
,且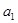 、
、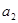 、
、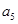 成等比数列,则数列
成等比数列,则数列 是等比数列,且
是等比数列,且 则
则
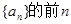 项和为
项和为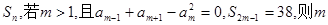 =
=