题目内容
(本小题满分12分)已知函数f(x)=x3+x2-2.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值.
解析:
(1)证明:因为f(x)=x3+x2-2,
所以f′(x)=x2+2x,
由点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,得an+12-2an+1=an2+2an,即(an+1+an)(an+1-an-2)=0.
又an>0(n∈N*),所以an+1-an=2.
又因为a1=3,
所以数列{an}是以3为首项,以2为公差的等差数列,
所以Sn=3n+×2=n2+2n.
又因为f′(n)=n2+2n,所以Sn=f′(n),
故点(n,Sn)也在函数y=f′(x)的图象上.
(2)f′(x)=x2+2x=x(x+2),
由f′(x)=0,得x=0或x=-2,
当x变化时,f′(x)、f(x)的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |  ? ? | 极大值 |  ? ? | 极小值 |  ? ? |
①当a-1<-2<a,即-2<a<-1时,f(x)的极大值为f(-2)=-,此时f(x)无极小值;
②当a-1<0<a,即0<a<1时,f(x)的极小值为f(0)=-2,此时f(x)无极大值;
③当a≤-2或-1≤a≤0或a≥1时,f(x)既无极大值又无极小值.
略

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
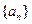 是递增数列,且满足
是递增数列,且满足 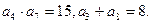
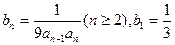 ,求数列
,求数列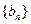 的前
的前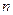 项和
项和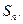
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列. n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.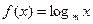 (m为常数,m>0且
(m为常数,m>0且 )
) 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.  是等比数列;
是等比数列; ,且数列{bn}的前n项和
,且数列{bn}的前n项和 ,当
,当 时,求
时,求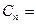
 ,问是否存在
,问是否存在 ,使得
,使得 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?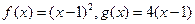 ,数列
,数列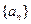 满足
满足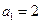 ,且
,且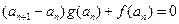 .
.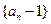 是否是等比数列?
是否是等比数列?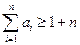 ;
;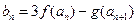 ,试探究数列
,试探究数列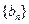 是否存在最大项和最小项?若存在求出
是否存在最大项和最小项?若存在求出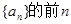 项和为
项和为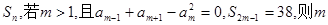 =
= ,若
,若 成等差数列(公差不为零),则
成等差数列(公差不为零),则