题目内容
4．在平面直角坐标系xOy中，设向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（0，-1），$\overrightarrow{c}$=（k，-2），若（$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k的值为8．分析 由题意可得（$\overrightarrow{a}$-2$\overrightarrow{b}$）•$\overrightarrow{c}$=（1，4）•（k，-2）=0，由此求得k的值．
解答 解：∵（$\overrightarrow{a}$-2$\overrightarrow{b}$）=（1，4），$\overrightarrow{c}$=（k，-2），（$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，
∴（$\overrightarrow{a}$-2$\overrightarrow{b}$）•$\overrightarrow{c}$=（1，4）•（k，-2）=k-8=0，求得k=8，
故答案为：8．
点评 本题主要考查两个向量的数量积公式，两个向量坐标形式的运算法则，两个向量垂直的性质，属于基础题
练习册系列答案
相关题目
如图，设F为抛物线y2=2px（p＞0）的焦点，P是抛物线上一定点，其坐为（x0，y0）（x0≠0），Q为线段OF的垂直平分线上一点，且点Q到抛物线的准线l的距离为$\frac{3}{2}$．
15．已知△ABC中，角A，B，C所对的边分别为a，b，c，且b+c=8，1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$，则△ABC面积的最大值为（ ）
| A． | 4 | B． | 4$\sqrt{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |
19．
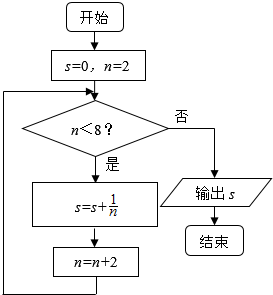如图所示，程序框图的输出结果是（ ）
如图所示，程序框图的输出结果是（ ）| A． | $\frac{1}{16}$ | B． | $\frac{25}{24}$ | C． | $\frac{11}{12}$ | D． | $\frac{3}{4}$ |
9．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与抛物线y2=4x的焦点重合，则a+b的最大值为（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{\sqrt{2}}{2}$ | D． | 2$\sqrt{2}$ |
如图，直线PQ与⊙O相切于点A，AB是⊙O的弦，∠PAB的平分线AC交⊙O于点C，连结CB，并延长与直线PQ相交于点Q，若AQ=6，AC=5．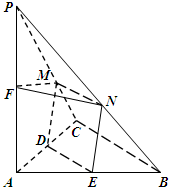
如图，在三棱锥P-ABC中，PA⊥平面ABC，2AC=2BC=PC=2，AC⊥BC，D、E、F分别为AC、AB、AP的中点，M、N分别为线段PC、PB上的动点，且有MN∥BC．