题目内容
14．
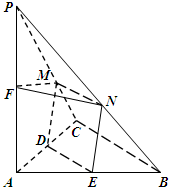如图，在三棱锥P-ABC中，PA⊥平面ABC，2AC=2BC=PC=2，AC⊥BC，D、E、F分别为AC、AB、AP的中点，M、N分别为线段PC、PB上的动点，且有MN∥BC．（Ⅰ）求证：MN⊥平面PAC；
（Ⅱ）当M为线段PC的中点时，求DM与平面PBC所成角的正弦值；
（Ⅲ）探究：是否存在这样的动点M，使得二面角E-MN-F为直二面角？若存在，求CM的长度；若不存在，说明理由．
分析 （Ⅰ）证明：BC⊥平面PAC，利用MN∥BC，即可证明MN⊥平面PAC；
（Ⅱ）以C为坐标原点，CA，CB所在直线为x，y轴，过C作平面ABC的垂线为z轴，建立坐标系，求出平面PBC的法向量，利用向量的夹角公式，求求DM与平面PBC所成角的正弦值；
（Ⅲ）由条件可得，∠FMD即为二面角E-MN-F的平面角，在△MDC中，由余弦定理建立方程，即可求CM的长度．
解答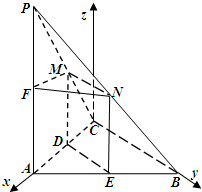 
（Ⅰ）证明：∵PA⊥平面ABC，
∴PA⊥BC，
又AC⊥BC，∴BC⊥面PAC．
又∵MN∥BC，
∴MN⊥面PAC．…（4分）
（Ⅱ）解：由已知CA⊥CB，以C为坐标原点，CA，CB所在直线为x，y轴，过C作平面ABC的垂线为z轴，作如图所示的坐标系．则$D（\frac{1}{2}，0，0）$，$M（\frac{1}{2}，0，\frac{{\sqrt{3}}}{2}）$，$P（1，0，\sqrt{3}）$，B（0，1，0）$\overrightarrow{DM}=（0，0，\frac{{\sqrt{3}}}{2}）$，$\overrightarrow{CP}=（1，0，\sqrt{3}）$，$\overrightarrow{CB}=（0，1，0）$
设平面PBC的法向量为u=（x，y，z），则$\left\{\begin{array}{l}\overrightarrow{CP}⊥u\\ \overrightarrow{CB}⊥u\end{array}\right.$，令z=1，解得$x=-\sqrt{3}，y=0$．
∴$u=（-\sqrt{3}，0，1）$，
设DM与平面PBC所成角为θ，
则sinθ=$|{cos＜u，\overrightarrow{DM}＞}|$=$\frac{{\frac{{\sqrt{3}}}{2}}}{{\frac{{\sqrt{3}}}{2}×2}}=\frac{1}{2}$．
则DM与平面PBC所成角为$\frac{π}{6}$．…（9分）
（Ⅲ）解：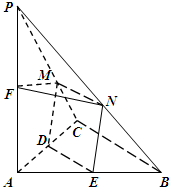
由条件可得，∠FMD即为二面角E-MN-F的平面角；
若二面角E-MN-F为直二面角，则∠FMD=90°．
在直角三角形PCA中，设CM=t，（0≤t≤2），则PM=2-t，
在△MDC中，由余弦定理可得，$D{M^2}=C{M^2}+C{D^2}-2CM•CDcos60°={t^2}+\frac{1}{4}-\frac{1}{2}t$；
同理可得，$F{M^2}=P{M^2}+P{F^2}-2PM•PFcos30°={（2-t）^2}+\frac{3}{4}-\frac{3}{2}（2-t）$．
又由FD2=FM2+MD2，得2t2-3t+1=0，解得t=1或$t=\frac{1}{2}$．
∴存在直二面角E-MN-F，且CM的长度为1或$\frac{1}{2}$．…（14分）
点评 本题考查线面垂直的判定，考查线面角，考查二面角的平面角，考查学生分析解决问题的能力，属于中档题．
