题目内容
16.设△ABC的内角A、B、C所对的边分别为a、b、c,且a+b=6,c=2,cosC=$\frac{7}{9}$.(Ⅰ)求a、b的值;
(Ⅱ)求sin(A-C)的值.
分析 (Ⅰ)根据余弦定理建立方程关系即可求a、b的值;
(Ⅱ)利用两角和差的正弦公式即可求sin(A-C)的值.
解答 解:(Ⅰ)由余弦定理c2=a2+b2-2abcosC,得c2=(a+b)2-2ab(1+cosC),
又a+b=6,c=2,cosC=$\frac{7}{9}$,
所以ab=9,解得a=3,b=3.…(6分)
(Ⅱ)在△ABC中,sinC=$\sqrt{1-co{s}^{2}B}$=$\frac{4\sqrt{2}}{9}$,
由正弦定理得sinA=$\frac{asinC}{c}$=$\frac{2\sqrt{2}}{3}$,
因为a=c,所以A为锐角,所以cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{1}{3}$,
因此 sin(A-C)=sinAcosC-cosAsinC=$\frac{10\sqrt{2}}{27}$.…(12分)
点评 本题主要考查三角函数值的计算,利用余弦定理和正弦定理以及两角和差的正弦公式是解决本题的关键.

练习册系列答案
相关题目
6.某单位计划在下月1日至7日举办人才交流会,某人随机选择其中的连续两天参加交流会,取么他在1日至3日期间连续两天参加交流会的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
7.已知命题p:若$\overrightarrow{a}$是非零向量,λ是非零实数,则$\overrightarrow{a}$与-λ$\overrightarrow{a}$方向相反;命题q:|-λ$\overrightarrow{a}$|=|λ|•$\overrightarrow{a}$.则下列命题为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∨q | D. | p∧(¬q) |
11.运行如下程序框图,如果输入的x∈(-∞,1],则输出的y属于( )
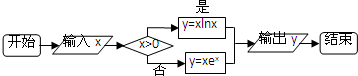

| A. | [-$\frac{1}{e}$,0] | B. | [-$\frac{1}{e}$,0) | C. | [-$\frac{1}{e}$,+∞) | D. | [-$\frac{1}{e}$,e) |