题目内容
12.已知方程$\frac{x^2}{4-m}+\frac{y^2}{m-1}$=1(m是常数)表示曲线C,给出下列命题:①曲线C不可能为圆;
②曲线C不可能为抛物线;
③若曲线C为双曲线,则m<1或m>4;
④若曲线C为焦点在x轴上的椭圆,则1<m<$\frac{5}{2}$.
其中真命题的编号为②③④.
分析 对选项分别进行判断,即可得出结论.
解答 解:①由4-m=m-1,可得m=2.5,曲线能为圆,故不正确;
②因为方程中没有一次项,故曲线C不可能为抛物线,正确;
③若曲线C为双曲线,(4-m)(m-1)<0,则m<1或m>4,正确;
④若曲线C为焦点在x轴上的椭圆,则4-m>m-1>0,所以1<m<$\frac{5}{2}$,正确.
故答案为:②③④.
点评 本题考查圆锥曲线的共同性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.有2000名网购者在11月11日当天于某购物网站进行网购消费(每人消费金额不超过 1000元),其中有女士1100名,男士900名,该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分折,如下表(消费金額卑位:元)
女士消费情况:
男士消费情况况:
(1)计算算x,y的值;在抽出的200名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者都是男士的概率;
(2)若消费金额不低于600元的网购者为“网购达人,低于600元的网购者为“非网购达人”根据以上统计数据填写答题卡中的2×2列联表,并冋答能否在犯错误的概率不超过0.05的前提下认为“是否为网购达人与性别有关?”
附表:
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
女士消费情况:
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800,1000] |
| 人数 | 10 | 25 | 35 | 30 | X |
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800.1000] |
| 人数 | 15 | 30 | 25 | Y | 5 |
(2)若消费金额不低于600元的网购者为“网购达人,低于600元的网购者为“非网购达人”根据以上统计数据填写答题卡中的2×2列联表,并冋答能否在犯错误的概率不超过0.05的前提下认为“是否为网购达人与性别有关?”
附表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
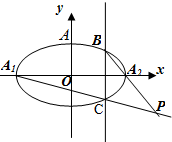 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.