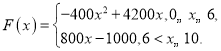题目内容
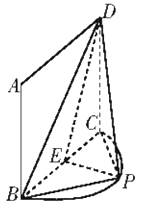
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)由面面垂直的性质定理,可得![]() 平面
平面![]() ,进而有
,进而有![]() ,再由已知可得,
,再由已知可得,![]() ,即可得证结论;
,即可得证结论;
(2)由体积公式,要使三棱锥![]() 的体积最大时,
的体积最大时,![]() 为弧
为弧![]() 的中点,求出
的中点,求出![]() ,进而求出
,进而求出![]() ,用等体积法
,用等体积法![]() ,即可求解.
,即可求解.
(1)证明:因为平面![]() 平面
平面![]() 是正方形,
是正方形,
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为点![]() 在以
在以![]() 为直径的半圆弧上,所以
为直径的半圆弧上,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)当点![]() 位于
位于![]() 的中点时,
的中点时,![]() 的面积最大,
的面积最大,
三棱锥![]() 的体积也最大.
的体积也最大.
因为![]() ,所以
,所以![]() ,
,
所以![]() 的面积为
的面积为![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() .
.
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]()
.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】一汽车厂生产![]() ,
,![]() ,
,![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() ,记这8辆轿车的得分的平均数为
,记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() ,且函数
,且函数![]() 没有零点
没有零点![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: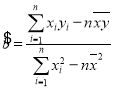 ,
,![]() .
.