题目内容
经过双曲线x2-y2=8的右焦点且斜率为2的直线被双曲线截得的线段的长是( )
A.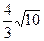 | B.2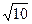 | C.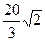 | D.7 |
C
双曲线x2-y2=8,右焦点F2(4,0),过F2斜率为2的直线方程为y=2(x-4),代入x2-y2=8中,消去y得3x2-32x+72=0,据弦长公式|AB|=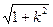 |x1-x2|=
|x1-x2|=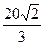 .
.
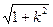 |x1-x2|=
|x1-x2|=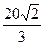 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
A.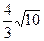 | B.2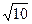 | C.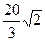 | D.7 |
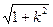 |x1-x2|=
|x1-x2|=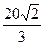 .
.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案