题目内容
【题目】已知![]() 为定义在
为定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,有
时,有![]() ,且当
,且当![]() 时,
时,![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.![]() B.函数
B.函数![]() 在定义域上是周期为
在定义域上是周期为![]() 的函数
的函数
C.直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点D.函数
个交点D.函数![]() 的值域为
的值域为![]()
【答案】A
【解析】
推导出当![]() 时,
时,![]() ,结合题中等式得出
,结合题中等式得出![]() ,可判断出A选项的正误;利用特殊值法可判断B选项的正误;作出函数
,可判断出A选项的正误;利用特殊值法可判断B选项的正误;作出函数![]() 在区间
在区间![]() 上的图象,利用数形结合思想可判断C选项的正误;求出函数
上的图象,利用数形结合思想可判断C选项的正误;求出函数![]() 在
在![]() 上的值域,利用奇函数的性质可得出函数
上的值域,利用奇函数的性质可得出函数![]() 的值域,可判断出D选项的正误.
的值域,可判断出D选项的正误.
![]() 函数
函数![]() 是
是![]() 上的奇函数,
上的奇函数,![]() ,由题意可得
,由题意可得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,A选项正确;
,A选项正确;
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则函数![]() 不是
不是![]() 上周期为
上周期为![]() 的函数,B选项错误;
的函数,B选项错误;
若![]() 为奇数时,
为奇数时,![]() ,
,
若![]() 为偶数,则
为偶数,则![]() ,即当
,即当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,若
,若![]() ,且当
,且当![]() 时,
时,![]() ,
,
![]() ,
,
当![]() 时,则
时,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
所以,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
由奇函数的性质可知,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
由此可知,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,D选项错误;
,D选项错误;
如下图所示:
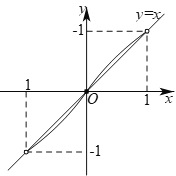
由图象可知,当![]() 时,函数
时,函数![]() 与函数
与函数![]() 的图象只有一个交点,
的图象只有一个交点,
当![]() 或
或![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 与函数
与函数![]() 没有交点,
没有交点,
则函数![]() 与函数
与函数![]() 有且只有一个交点,C选项错误.
有且只有一个交点,C选项错误.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目