题目内容
【题目】已知:函数f(x)=2lnx﹣ax2+3x,其中a∈R.
(1)若f(1)=2,求函数f(x)的最大值;
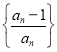
(2)若a=﹣1,正实数x1,x2满足f(x1)+f(x2)=0,证明:![]() .
.
【答案】(1)f(x)max=2ln2+2(2)证明见解析
【解析】
(1)计算得到![]() ,求导得到函数的单调区间,再计算最大值得到答案.
,求导得到函数的单调区间,再计算最大值得到答案.
(2)代入数据得到![]() ,得到
,得到![]() ,设
,设![]() 得到函数的最小值得到不等式(x1+x2)2+3(x1+x2)≥2,计算得到答案.
得到函数的最小值得到不等式(x1+x2)2+3(x1+x2)≥2,计算得到答案.
(1)∵f(1)=2,∴﹣a+3=2,∴a=1,∴f(x)=2lnx﹣x2+3x,
∴f'(x)![]() 2x+3
2x+3![]() ,
,
由f'(x)>0得,0<x<2,有f'(x)<0得,x>2,
∴f(x)在(0,2)为增函数,在(2,+∞)为减函数,
∴f(x)max=f(2)=2ln2+2;
(2)证明:当a=﹣1,f(x)=2lnx+x2+3x,
∵f(x1)+f(x2)=2lnx1+x12+3x1+2lnx2+x22+3x2=0,
∴(x1+x2)2+3(x1+x2)=2(x1x2﹣lnx1x2),
令h(t)=t﹣lnt,∴h'(t)=1![]() ,
,
由h'(x)>0得,t>1,由h'(x)<0得,0<t<1,
∴h(x)在(0,1)上为减函数,在(1,+∞)上为增函数,
∴h(x)min=h(1)=1,∴(x1+x2)2+3(x1+x2)≥2,
∴(x1+x2)2+3(x1+x2)﹣2≥0,
解得:![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目