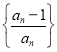
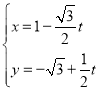题目内容
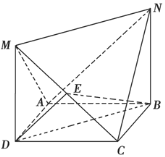
【题目】如图,已知四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为MC的中点,则下列结论不正确的是( )
A. 平面![]() 平面ABN B.
平面ABN B. ![]()
C. 平面![]() 平面AMN D. 平面
平面AMN D. 平面![]() 平面AMN
平面AMN
【答案】C
【解析】
将几何体补成正方体后再进行判断.
分别过A,C作平面ABCD的垂线AP,CQ,使得AP=CQ=1,连接PM,PN,QM,QN,将几何体补成棱长为1的正方体.

∵BC⊥平面ABN,BC平面BCE,
∴平面BCE⊥平面ABN,故A正确;
连接PB,则PB∥MC,显然PB⊥AN,∴MC⊥AN,故B正确;
取MN的中点F,连接AF,CF,AC.
∵△AMN和△CMN都是边长为![]() 的等边三角形,
的等边三角形,
∴AF⊥MN,CF⊥MN,
∴∠AFC为二面角A-MN-C的平面角,
∵AF=CF=![]() ,AC=
,AC=![]() ,∴AF2+CF2≠AC2,即∠AFC≠
,∴AF2+CF2≠AC2,即∠AFC≠![]() ,
,
∴平面CMN与平面AMN不垂直,故C错误;
∵DE∥AN,MN∥BD,
∴平面BDE∥平面AMN,故D正确.
故选C.

 阅读快车系列答案
阅读快车系列答案【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统 计,在2018年这一年内从![]() 市到
市到![]() 市乘坐高铁或飞机出行的成年人约为
市乘坐高铁或飞机出行的成年人约为![]() 万人次.为了 解乘客出行的满意度,现从中随机抽取
万人次.为了 解乘客出行的满意度,现从中随机抽取![]() 人次作为样本,得到下表(单位:人次):
人次作为样本,得到下表(单位:人次):
满意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | |
10分(满意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不满意) | 1 | 0 | 6 | 3 | 4 | 4 |
(span>1)在样本中任取![]() 个,求这个出行人恰好不是青年人的概率;
个,求这个出行人恰好不是青年人的概率;
(2)在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,记其中老年人出行的人次为
人次,记其中老年人出行的人次为![]() .以频率作为概率,求
.以频率作为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)如果甲将要从![]() 市出发到
市出发到![]() 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况和优惠活动评价的
条较为详细的评价信息进行统计,车辆状况和优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送每张的面额为
向用户随机派送每张的面额为![]() 元,
元,![]() 元,
元,![]() 元的三种骑行券,用户每次使用
元的三种骑行券,用户每次使用![]() 扫码用车后,都可获得一张骑行券,用户骑行一-次获得
扫码用车后,都可获得一张骑行券,用户骑行一-次获得![]() 元券,获得
元券,获得![]() 元券的概率分别是
元券的概率分别是![]() ,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
附:下边的临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: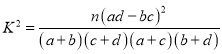 ,其中
,其中![]() )
)