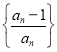
题目内容
【题目】已知椭圆
的焦距为4，且过点
.
（1）求椭圆
的标准方程；
（2）设
为椭圆上一点，过点
作
轴的垂线，垂足为
，取点
，连接
，过点
作的垂线交轴于点
，点
是点关于
轴的对称点，作直线
，问这样作出的直线是否与椭圆一定有唯一的公共点？并说明理由.
【答案】(1) 
(2) 直线
与椭圆
一定有唯一的公共点，见解析
【解析】
（1）根据题意得到关于
、
的方程组，解得.
（2）由题意，
点坐标为
，设
，由
知，
求出
，根据对称表示出
点坐标，即可表示出直线
的方程，联立直线与椭圆方程消元可得.
解：（1）因为焦距为4，所以
，又因为椭圆过点
，
所以
，故
，
，从而椭圆的方程为
已知椭圆
的焦距为4，且过点.
（2）由题意，点坐标为，设，则
，
，再由知，，即
.
由于
，故
，因为点是点
关于
轴的对称点，所以点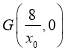
.
故直线的斜率
.
又因
在椭圆上，所以
.①
从而
，故直线的方程为
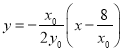②
将②代入椭圆方程，得
③
再将①代入③，化简得：
解得
，
，即直线与椭圆一定有唯一的公共点.
名师点拨卷系列答案
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展，下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量（万台） | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况，得到的部分数据如下表所示：
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
（1）求新能源乘用车的销量
关于年份
的线性相关系数
，并判断与是否线性相关；
（2）请将上述
列联表补充完整，并判断是否有
的把握认为购车车主是否购置新能源乘用车与性别有关；
参考公式：
，
，其中
.
，若
，则可判断与线性相关.
附表：
| 0．10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
