题目内容
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(1)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(3)若![]() 为正整数,函数
为正整数,函数![]() 恰好有两个零点,求
恰好有两个零点,求![]() 的值.
的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)由题意得出![]() ,即可求出实数
,即可求出实数![]() 的值;
的值;
(2)由![]() ,可得出
,可得出![]() ,对
,对![]() 与
与![]() 的大小关系进行分类讨论,分析导数的符号,可得出函数
的大小关系进行分类讨论,分析导数的符号,可得出函数![]() 的单调增区间和减区间;
的单调增区间和减区间;
(3)分![]() 、
、![]() 和
和![]() 三种情况讨论,结合(2)中函数
三种情况讨论,结合(2)中函数![]() 的单调性以及零点存在定理来判断出函数
的单调性以及零点存在定理来判断出函数![]() 的零点个数,可得出整数
的零点个数,可得出整数![]() 的值.
的值.
(1)由题意![]() ,
,![]() ,则
,则![]() ,
,
由于函数![]() 的图象在
的图象在![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,
则![]() ,所以
,所以![]() ,因此,
,因此,![]() ;
;
(2)![]() ,则
,则![]() .
.
①若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
②若![]() 时,
时,![]() ,对
,对![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递增;
单调递增;
③若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
(3)因为![]() 为正整数,
为正整数,
若![]() ,则
,则![]() ,
,![]() ,
,
由(2)知![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
又![]() ,所以
,所以![]() 在区间
在区间![]() 内仅有
内仅有![]() 实根,
实根,![]() ,
,
又![]() ,所以
,所以![]() 在区间
在区间![]() 内仅有
内仅有![]() 实根.
实根.
此时,![]() 在区间
在区间![]() 内恰有
内恰有![]() 实根;
实根;
若![]() ,
,![]() 在
在![]() 单调递增,至多有
单调递增,至多有![]() 实根.
实根.
若![]() ,
,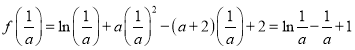 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
由(2)知![]() 在
在![]() 单调递减,在
单调递减,在![]() 和
和![]() 单调递增,
单调递增,
所以![]() ,所以
,所以![]() 在
在![]() 至多有
至多有![]() 实根.
实根.
综上,![]() .
.

 考前必练系列答案
考前必练系列答案【题目】为了节能减排,发展低碳经济,我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表 | ||||
新能源汽车生产情况 | 新能源汽车销售情况 | |||
产品(万辆) | 比上年同期 | 销量(万辆) | 比上年同期 | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
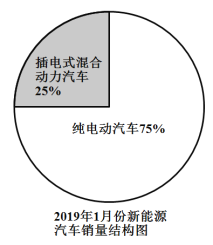
根据上述图表信息,下列结论错误的是( )
A.2017年3月份我国新能源汽车的产量不超过![]() 万辆
万辆
B.2017年我国新能源汽车总销量超过![]() 万辆
万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于![]() 万辆
万辆
【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统 计,在2018年这一年内从![]() 市到
市到![]() 市乘坐高铁或飞机出行的成年人约为
市乘坐高铁或飞机出行的成年人约为![]() 万人次.为了 解乘客出行的满意度,现从中随机抽取
万人次.为了 解乘客出行的满意度,现从中随机抽取![]() 人次作为样本,得到下表(单位:人次):
人次作为样本,得到下表(单位:人次):
满意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | |
10分(满意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不满意) | 1 | 0 | 6 | 3 | 4 | 4 |
(span>1)在样本中任取![]() 个,求这个出行人恰好不是青年人的概率;
个,求这个出行人恰好不是青年人的概率;
(2)在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,记其中老年人出行的人次为
人次,记其中老年人出行的人次为![]() .以频率作为概率,求
.以频率作为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)如果甲将要从![]() 市出发到
市出发到![]() 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
