题目内容
(本题11分)
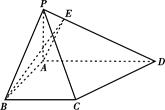
如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点. (1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值.(3)求B点到面ECD的距离
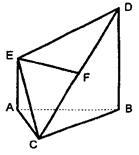
如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点. (1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值.(3)求B点到面ECD的距离


(3)
建立如图坐标系
E(0,
 ,0) C(-1,0,0) D(1,0,2)
,0) C(-1,0,0) D(1,0,2)B(1,0,0) EC=(-1,-
 ,-1)
,-1)CD=(2,0,2) CB=(-2,0,0)
面ECD法向量n="(1,0,-1) "
则

所以。所求距离为

略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
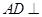 平面ABE
平面ABE ,BE=BC,F为CE上的点,且
,BE=BC,F为CE上的点,且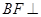 平面ACE。
平面ACE。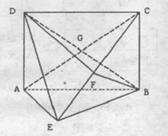
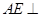 平面BCE;
平面BCE;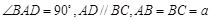 ,
,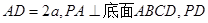 与底面成30°角.
与底面成30°角.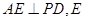 为垂足,求证:
为垂足,求证: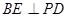 ;
;
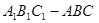 中,
中,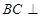 侧面
侧面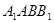 ,且
,且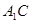 与底面成
与底面成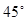 角,
角,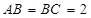 ,则该棱柱体积的 最小值为 .
,则该棱柱体积的 最小值为 .  .
.
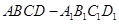 中,
中,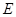 为
为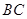 的中点,
的中点,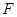 为
为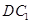 的中点.
的中点.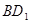 //平面
//平面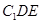 ;(2)求三棱锥
;(2)求三棱锥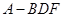 的体积;
的体积;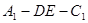 的余弦值。
的余弦值。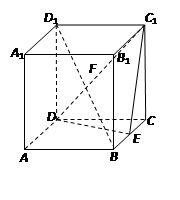
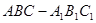 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,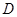 为
为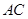 的中点.
的中点.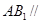 平面
平面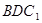 ;
;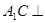 平面
平面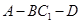 的正切值.
的正切值.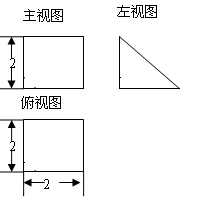
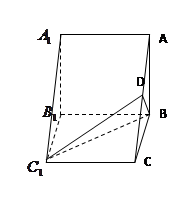
 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。
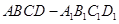 中,
中,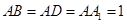 ,
, 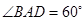 ,
,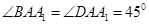 ,
,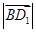 ;
;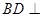 平面
平面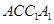 .
.