题目内容
(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD为菱形,PD=AD,∠DAB="60°," PD⊥底面ABCD.
(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3) 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。

(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3)
 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。
文)(1) 底面ABCD为菱形,
底面ABCD为菱形,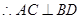 ,
, PD⊥底面ABCD,
PD⊥底面ABCD,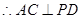 ,
,
 ,
, (4分)
(4分)
(2)设PD=AD=1,设A到平面PBC的距离为h,则由题意PA=PB=PC= ,
,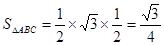
在等腰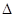 PBC中,可求
PBC中,可求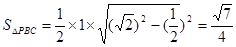
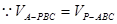 ,
, ,可得h=
,可得h=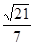 ,
,
 (12分)
(12分)
(理)(1)过P作BC的平行线L即为所求。(2分)因为BC∥A D,
D,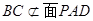 ,
, ,所以BC∥平面PAD,因为平面PAD
,所以BC∥平面PAD,因为平面PAD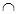 平面PBC=L,所以BC∥L (5分)
平面PBC=L,所以BC∥L (5分)
(2)设PD=AD=1,由题意可知,PA=PB=PC= ,取BC中点M,连PM、DM,则PM⊥BC,因为PD⊥BC,又BC∥L,所以
,取BC中点M,连PM、DM,则PM⊥BC,因为PD⊥BC,又BC∥L,所以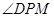 为所求。(8分)在
为所求。(8分)在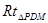 中,
中,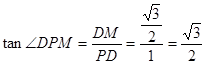 (12分)
(12分)
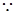 底面ABCD为菱形,
底面ABCD为菱形,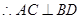 ,
,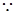 PD⊥底面ABCD,
PD⊥底面ABCD,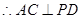 ,
,
 ,
, (4分)
(4分)(2)设PD=AD=1,设A到平面PBC的距离为h,则由题意PA=PB=PC=
 ,
,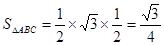
在等腰
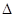 PBC中,可求
PBC中,可求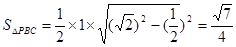
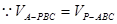 ,
, ,可得h=
,可得h=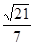 ,
, (12分)
(12分)(理)(1)过P作BC的平行线L即为所求。(2分)因为BC∥A
 D,
D,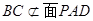 ,
, ,所以BC∥平面PAD,因为平面PAD
,所以BC∥平面PAD,因为平面PAD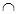 平面PBC=L,所以BC∥L (5分)
平面PBC=L,所以BC∥L (5分)(2)设PD=AD=1,由题意可知,PA=PB=PC=
 ,取BC中点M,连PM、DM,则PM⊥BC,因为PD⊥BC,又BC∥L,所以
,取BC中点M,连PM、DM,则PM⊥BC,因为PD⊥BC,又BC∥L,所以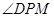 为所求。(8分)在
为所求。(8分)在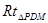 中,
中,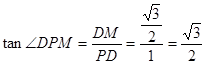 (12分)
(12分)略

练习册系列答案
相关题目
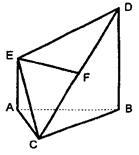
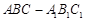 的底面是直角三角形,
的底面是直角三角形,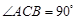 ,侧棱与底面所成角为
,侧棱与底面所成角为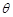 ,点
,点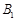 在底面上射影D落在BC上.
在底面上射影D落在BC上.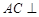 平面
平面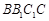 ;
;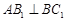 ,求
,求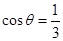 ,且当
,且当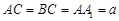 时,求二面角
时,求二面角 的大小.
的大小.
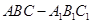 中,
中,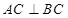 ,点
,点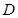 是
是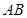 的中点.
的中点.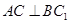 ;(2)
;(2)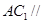 平面
平面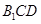 .
.
 中,
中,  ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
;
 是边长为
是边长为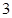 的正方形,
的正方形,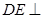 平面
平面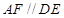 ,
,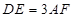 ,
,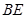 与平面
与平面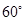 .
.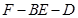 的余弦值;
的余弦值;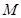 是线段
是线段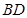 上的一个动点,问当
上的一个动点,问当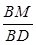 的值为多少时,可使得
的值为多少时,可使得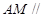 平面
平面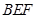 ,并证明你的结论.
,并证明你的结论.
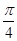 .
.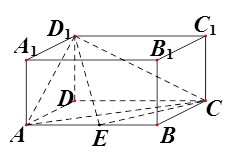





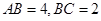 的矩形
的矩形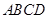 ,沿对角线
,沿对角线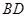 将
将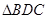 折起,使得面
折起,使得面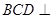 面
面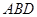 ,则异面直线
,则异面直线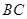 与
与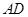 所成角的余弦值为
所成角的余弦值为