题目内容
如图,在三棱柱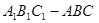 中,
中,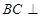 侧面
侧面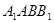 ,且
,且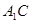 与底面成
与底面成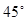 角,
角,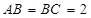 ,则该棱柱体积的 最小值为 .
,则该棱柱体积的 最小值为 .
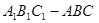 中,
中,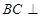 侧面
侧面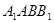 ,且
,且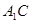 与底面成
与底面成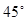 角,
角,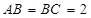 ,则该棱柱体积的 最小值为 .
,则该棱柱体积的 最小值为 . 4
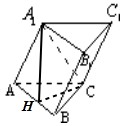
如图,过点
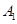 作
作 ,连接
,连接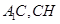
因为
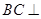 侧面
侧面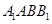 ,所以
,所以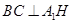 ,从而有
,从而有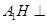 面
面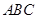
所以
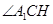 是
是 与底面所成角,故
与底面所成角,故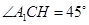 ,则
,则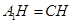
因为底面
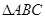 面积固定,所以当
面积固定,所以当 最小即
最小即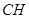 最小时,棱柱体积取到最小值
最小时,棱柱体积取到最小值因为
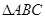 是等腰直角三角形,所以当
是等腰直角三角形,所以当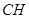 与
与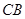 重合时,
重合时,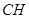 最小
最小此时
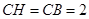 ,三棱柱体积
,三棱柱体积

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
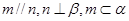 ,则
,则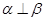
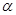
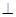
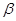 ,
,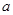
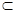
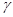 ,
,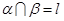 ,则
,则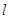
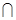
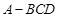 中,
中,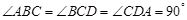 ,
,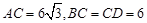 ,
,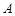 在底面
在底面 上的射影为
上的射影为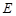 .
.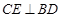 ;
;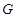 在棱
在棱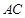 上,且
上,且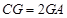 ,
,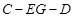 的余弦值
的余弦值 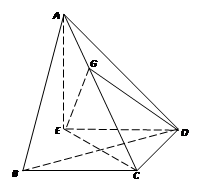
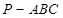 中,
中,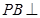 底面
底面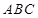 ,
,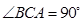 ,
,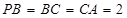 ,
,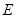 为
为 的中点,点
的中点,点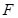 在
在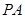 上,且
上,且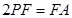 .
.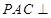 平面
平面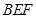 ;
; 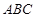 与平面
与平面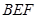 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.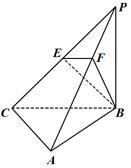
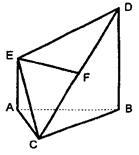
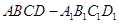 中,
中, 与平面
与平面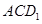 所成角的余弦值为( ▲ )
所成角的余弦值为( ▲ )

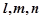 是三条不同的直线,
是三条不同的直线,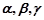 是三个不同的平面,则下列命题中为假命题的是
是三个不同的平面,则下列命题中为假命题的是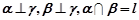 ,则
,则
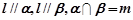 ,则
,则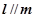
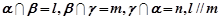 ,则
,则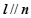
 ,则
,则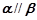 或
或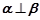
 中
中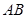 ‖
‖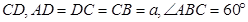 ,平面
,平面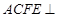 平面
平面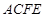 是矩形,
是矩形,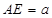 ,点
,点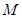 在线段
在线段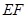 上.
上.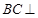 平面
平面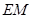 为何值时,
为何值时,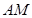 ‖平面
‖平面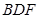 ?证明你的结论;
?证明你的结论;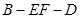 的大小.
的大小. 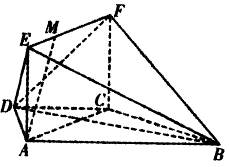
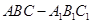 中,
中,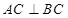 ,点
,点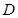 是
是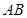 的中点.
的中点.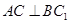 ;(2)
;(2)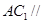 平面
平面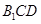 .
.