题目内容
已知正四面体ABCD的棱长为2,所有与它的四个顶点距离相等的平面截这个四面体所得截面的面积之和是
( )
( )
A.3+
| B.4 | C.3 | D.
|
设E、F、G分别为AB、AC、AD的中点,连结EF、FG、GE,
则△EFG是三棱锥A-BCD的中截面,
可得平面EFG∥平面BCD,点A到平面EFG的距离等于平面EFG与平面BCD之间的距离,
∴A、B、C、D到平面EFG的距离相等,即平面EFG是到四面体ABCD四个顶点距离相等的一个平面.
正四面体ABCD中,象△EFG这样的三角形截面共有4个.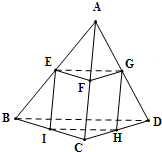
∵正四面体ABCD的棱长为2,可得EF=FG=GE=1,
∴△EFG是边长为1的正三角形,可得S△EFG=
EF•FG•sin60°=
.
取CD、BC的中点H、I,连结GH、HI、IE,
∵EI、GH分别是△ABC、△ADC的中位线,
∴EI
AC,GH
AC,得EI
GH,可得四边形EGHI为平行四边形,
又∵AC=BD且AC⊥BD,EI
AC,HI
BD,
∴EI=HI且EI⊥HI,可得四边形EGHI为正方形,其边长为
AC=1,由此可得正方形EGHI的面积SEGHI=1.
∵BC的中点I在平面EGHI内,∴B、C两点到平面EGHI的距离相等.
同理可得D、C两点到平面EGHI的距离相等,且A、B两点到平面EGHI的距离相等.
∴A、B、C、D到平面EGHI的距离相等,可得平面EGHI是到四面体ABCD四个顶点距离相等的一个平面.
正四面体ABCD中,象四边形EGHI这样的正方形截面共有3个.
因此,所有满足条件的正四面体的截面面积之和等于4S△EFG+3SEGHI=4×
+3×1=3+
.
故选:A
则△EFG是三棱锥A-BCD的中截面,
可得平面EFG∥平面BCD,点A到平面EFG的距离等于平面EFG与平面BCD之间的距离,
∴A、B、C、D到平面EFG的距离相等,即平面EFG是到四面体ABCD四个顶点距离相等的一个平面.
正四面体ABCD中,象△EFG这样的三角形截面共有4个.

∵正四面体ABCD的棱长为2,可得EF=FG=GE=1,
∴△EFG是边长为1的正三角形,可得S△EFG=
| 1 |
| 2 |
| ||
| 4 |
取CD、BC的中点H、I,连结GH、HI、IE,
∵EI、GH分别是△ABC、△ADC的中位线,
∴EI
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
又∵AC=BD且AC⊥BD,EI
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
∴EI=HI且EI⊥HI,可得四边形EGHI为正方形,其边长为
| 1 |
| 2 |
∵BC的中点I在平面EGHI内,∴B、C两点到平面EGHI的距离相等.
同理可得D、C两点到平面EGHI的距离相等,且A、B两点到平面EGHI的距离相等.
∴A、B、C、D到平面EGHI的距离相等,可得平面EGHI是到四面体ABCD四个顶点距离相等的一个平面.
正四面体ABCD中,象四边形EGHI这样的正方形截面共有3个.
因此,所有满足条件的正四面体的截面面积之和等于4S△EFG+3SEGHI=4×
| ||
| 4 |
| 3 |
故选:A

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 ,
,

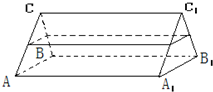
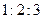 ,则它们的体积之比是_____________。
,则它们的体积之比是_____________。