题目内容
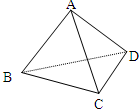
点A、B、C、D在同一球面上，AB=BC=
，AC=2，若四面体ABCD的体积的最大值为
，则这个球的表面积为（ ）
| 2 |
| 2 |
| 3 |
A．
| B．8π | C．
| D．
|
根据题意知，△ABC是一个直角三角形，其面积为1．其所在球的小圆的圆心在斜边AC的中点上，设小圆的圆心为Q，
若四面体ABCD的体积的最大值，由于底面积S△ABC不变，高最大时体积最大，
所以，DQ与面ABC垂直时体积最大，最大值为
×S△ABC×DQ=
，
即
×1×DQ=
，∴DQ=2，如图．
设球心为O，半径为R，则在直角△AQO中，
OA2=AQ2+OQ2，即R2=12+（2-R）2，∴R=
则这个球的表面积为：S=4π（
）2=
π；
故选C．
若四面体ABCD的体积的最大值，由于底面积S△ABC不变，高最大时体积最大，
所以，DQ与面ABC垂直时体积最大，最大值为
| 1 |
| 3 |
| 2 |
| 3 |
即
| 1 |
| 3 |
| 2 |
| 3 |
设球心为O，半径为R，则在直角△AQO中，
OA2=AQ2+OQ2，即R2=12+（2-R）2，∴R=
| 5 |
| 4 |
则这个球的表面积为：S=4π（
| 5 |
| 4 |
| 25 |
| 4 |
故选C．
练习册系列答案
相关题目
