题目内容
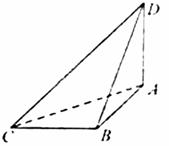
有棱长为6的正四面体SABC，A′，B′，C′分别在棱SA，SB，SC上，且SA′=2，SB′=3，SC′=4，则截面A′B′C′将此正四面体分成的两部分体积之比为（ ）
A．
| B．
| C．
| D．
|
∵棱长为a的正四面体的体积V=
a3
∴棱长为6的正四面体的体积V=18
∵棱长为a的正四面体的高h=
a，
∴棱长为6的正四面体的高h=2
B′在棱SB上，SB′=3，
故B′到面SA′C′的距离d=
又∵A′，C′分别在棱SA，SC上，SA′=2，SC′=4，
∴S△SA′C′=
×2×4×
=2
棱锥S′A′B′C′的体积V1=
S△SA′C′•d=2
故余下的几何体的体积V2=16
∴V1：V2=1：8
故选B
| ||
| 12 |
∴棱长为6的正四面体的体积V=18
| 2 |
∵棱长为a的正四面体的高h=
| ||
| 3 |
∴棱长为6的正四面体的高h=2
| 6 |
B′在棱SB上，SB′=3，
故B′到面SA′C′的距离d=
| 6 |
又∵A′，C′分别在棱SA，SC上，SA′=2，SC′=4，
∴S△SA′C′=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
棱锥S′A′B′C′的体积V1=
| 1 |
| 3 |
| 2 |
故余下的几何体的体积V2=16
| 2 |
∴V1：V2=1：8
故选B
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
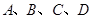，DA⊥平面ABC。AB⊥BC，DA=AB=BC=
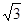，则球O的体积等于 。
