题目内容
8.设x>0,则函数y=x2+$\frac{4}{x}$的最小值为3$\root{3}{4}$.分析 由题意可得y=x2+$\frac{4}{x}$=x2+$\frac{2}{x}$+$\frac{2}{x}$,由基本不等式可得.
解答 解:∵x>0,∴函数y=x2+$\frac{4}{x}$=x2+$\frac{2}{x}$+$\frac{2}{x}$
≥3$\root{3}{{x}^{2}•\frac{2}{x}•\frac{2}{x}}$=3$\root{3}{4}$,
当且仅当x2=$\frac{2}{x}$即x=$\root{3}{2}$时取等号,
∴函数y=x2+$\frac{4}{x}$的最小值为:3$\root{3}{4}$,
故答案为:3$\root{3}{4}$
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.等差数列{an}中,a5=3,a17=2a8
(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}{a_n}}}(n∈{N^*})$,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}{a_n}}}(n∈{N^*})$,求数列{bn}的前n项和Sn.
17.一个几何体的三视图如图所示,则该几何体的体积是( )
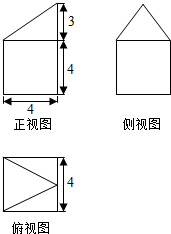

| A. | 64 | B. | 72 | C. | 80 | D. | 112 |
18.$\frac{1+cos20°}{2sin20°}$-sin10°(tan-15°-tan5°)=( )
| A. | $\sqrt{3}$ | B. | 1 | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
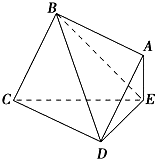 正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.
正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.