题目内容
20.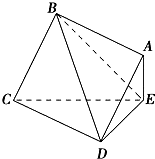 正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.
正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.
分析 (1)根据正方形对边平行可得AB∥CD,结合线面平行的判定定理可得AB∥平面CDE;
(2)由已知AE⊥平面CDE,可得AE⊥CD,结合正方形ABCD邻边垂直及线面垂直的判定定理可得CD⊥平面ADE,进而由面面垂直的判定定理可得平面ABCD⊥平面ADE.
解答 证明:(1)正方形ABCD中,AB∥CD,
又AB?平面CDE,
CD?平面CDE,
所以AB∥平面CDE.(6分)
(2)因为AE⊥平面CDE,
且CD?平面CDE,
所以AE⊥CD,(8分)
又正方形ABCD中,CD⊥AD
且AE∩AD=A,AE,AD?平面ADE,
所以CD⊥平面ADE,(12分)
又CD?平面ABCD,
所以平面ABCD⊥平面ADE.(14分
点评 本题考查的知识点是平面与平面垂直的判定,直线与平面垂直的判定与性质,直线与平面平行的判定,熟练掌握空间线面关系的判定定理是解答的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
17.直线4kx-4y-k=0与抛物线y2=x交于A,B两点,若|AB|=4,则弦AB的中点到直线x=-$\frac{1}{2}$的距离等于( )
| A. | $\frac{7}{4}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
11.在△ABC中,角A,B,C所对的边分别是a,b,c,若向量$\overrightarrow{p}$=(4,a2+b2-c2),$\overrightarrow{q}$=($\sqrt{3}$,$\frac{1}{2}$absinC),且满足$\overrightarrow{p}$∥$\overrightarrow{q}$,则C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
15.若(1+x)n的展开式中x2项的系数为an,则$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$的值( )
| A. | 一定大于2 | B. | 一定小于2 | C. | 等于2 | D. | 一定大于$\frac{3}{2}$ |
10.已知x与y之间的几组数据如下表:
假设根据上表数据所得线性回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,根据中间两组数据(4,3)和(5,4)求得的直线方程为y=bx+a,则$\widehat{b}$与b,$\widehat{a}$与a的大小为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{b}$>b,$\widehat{a}$>a | B. | $\widehat{b}$>b,$\widehat{a}$<a | C. | $\widehat{b}$<b,$\widehat{a}$>a | D. | $\widehat{b}$<b,$\widehat{a}$<a |