题目内容
(本小题满分14分)已知长方形 ,
,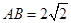 ,
,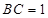 ,以
,以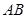 的中点
的中点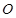 为
为
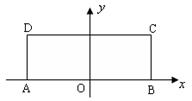
原点建立如图所示的平面直角坐标系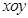 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中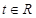 ,探究
,探究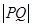 的最
的最
小值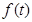 。
。
 ,
,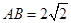 ,
,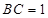 ,以
,以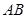 的中点
的中点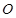 为
为原点建立如图所示的平面直角坐标系
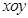 .
.(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中
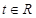 ,探究
,探究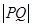 的最
的最小值
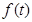 。
。
解:(1)由题意可得点A、B、C的坐标分别为 …………2分
…………2分
设椭圆的标准方程是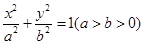
则: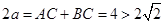 ,∴
,∴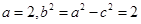 ……………………4分
……………………4分
∴椭圆的标准方程是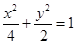 …………………6分
…………………6分
(2)设点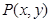 ,则
,则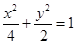 ,其中
,其中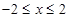
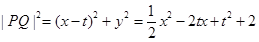 ,其中对称轴是
,其中对称轴是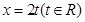 ……8分
……8分
当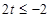 即
即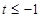 时,
时,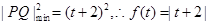 ;
;
当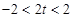 即
即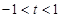 时,
时,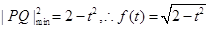 ;
;
当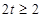 即
即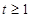 时,
时,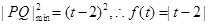 ;
;
综上所述: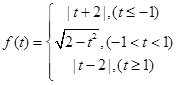 ………………………14分
………………………14分
 …………2分
…………2分设椭圆的标准方程是
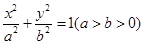
则:
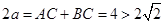 ,∴
,∴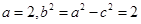 ……………………4分
……………………4分∴椭圆的标准方程是
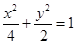 …………………6分
…………………6分(2)设点
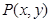 ,则
,则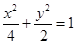 ,其中
,其中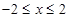
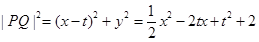 ,其中对称轴是
,其中对称轴是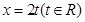 ……8分
……8分当
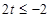 即
即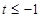 时,
时,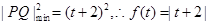 ;
;当
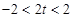 即
即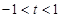 时,
时,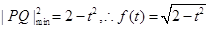 ;
;当
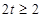 即
即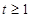 时,
时,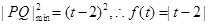 ;
;综上所述:
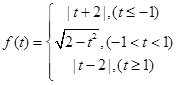 ………………………14分
………………………14分本题主要考查了利用椭圆的定义求解椭圆的参数a,c,b的值,进而求解椭圆的方程,及二次曲线表示椭圆、双曲线、圆的条件的考查.
(1)根据题意设出椭圆的方程,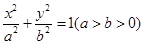 ,然后借助于
,然后借助于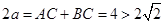 ,∴
,∴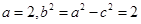 得到椭圆方程。
得到椭圆方程。
(2)设点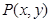 ,则
,则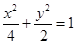 ,其中
,其中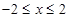
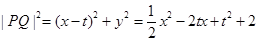 ,其中对称轴是
,其中对称轴是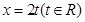 然后对于参数t讨论得到最值。
然后对于参数t讨论得到最值。
(1)根据题意设出椭圆的方程,
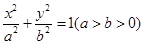 ,然后借助于
,然后借助于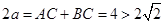 ,∴
,∴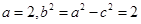 得到椭圆方程。
得到椭圆方程。(2)设点
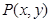 ,则
,则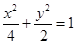 ,其中
,其中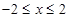
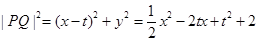 ,其中对称轴是
,其中对称轴是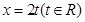 然后对于参数t讨论得到最值。
然后对于参数t讨论得到最值。
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
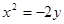 上有两点
上有两点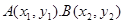 且
且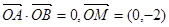 (0为坐标原点)
(0为坐标原点)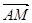 ∥
∥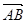 (2)若
(2)若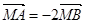 ,求AB所在直线方程。
,求AB所在直线方程。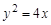 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线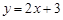 和
和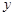 轴的距离之和的最小值
轴的距离之和的最小值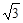
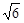
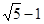
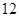 ,离心率为
,离心率为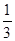 ,则椭圆的方程是( )
,则椭圆的方程是( )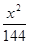 +
+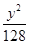 =1
=1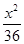 +
+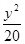 =1
=1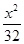 +
+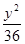 =1
=1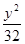 =1
=1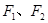 分别是双曲线
分别是双曲线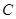 :
: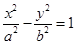 (
(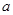 >0,
>0,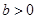 )的左、右焦点,
)的左、右焦点,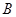 是虚轴的端点,直线
是虚轴的端点,直线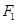
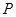 、
、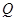 两点,线段
两点,线段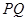 的垂直平分线与
的垂直平分线与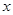 轴交于点
轴交于点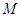 ,若
,若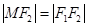 ,则
,则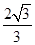
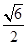
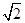
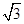
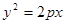 与直线
与直线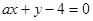 交于两点
交于两点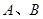 ,其中点
,其中点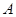 的坐标是
的坐标是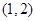 ,设抛物线的焦点为
,设抛物线的焦点为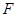 ,则
,则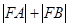 等于 ( )
等于 ( )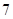
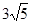
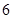
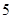
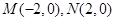 ,动点
,动点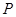 满足条件
满足条件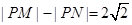 .记动点
.记动点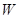 .
.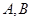 是
是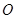 是坐标原点,求
是坐标原点,求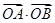 的最小值.
的最小值.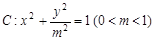 的左、右焦点分别为
的左、右焦点分别为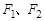 。过
。过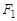 的直线
的直线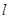 交
交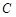 于
于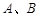 两点,且
两点,且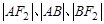 成等差数列.
成等差数列.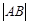 ; (2)若直线
; (2)若直线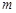 .
.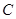 :
: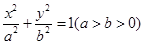 的离心率为
的离心率为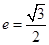 ,且过点
,且过点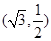 .
.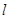 与椭圆
与椭圆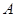 、
、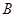 两点,若以
两点,若以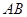 为直径的圆
为直径的圆 经过坐标原点.证明:圆
经过坐标原点.证明:圆