题目内容
已知椭圆的中心在原点,焦点在x轴上,且长轴长为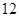 ,离心率为
,离心率为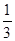 ,则椭圆的方程是( )
,则椭圆的方程是( )
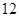 ,离心率为
,离心率为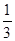 ,则椭圆的方程是( )
,则椭圆的方程是( )A.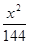 + +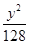 =1 =1 | B.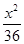 + +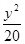 =1 =1 | C.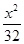 + +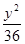 =1 =1 | D.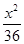 + +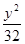 =1 =1 |
D
试题分析:因为椭圆的中心在原点,焦点在x轴上,所以设椭圆标准方程为:
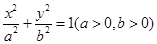 ,因为长轴长为
,因为长轴长为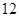 ,所以
,所以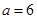 ,又因为离心率为
,又因为离心率为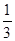 ,所以
,所以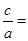
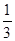 ,所以
,所以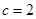 ,所以
,所以 所以椭圆的方程为
所以椭圆的方程为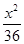 +
+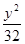 =1.
=1.点评:解题的关键在于掌握椭圆标准方程和基本量并熟练应用,比如长轴长是
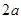 ,有的同学会误认为是
,有的同学会误认为是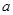 而导致计算错误.
而导致计算错误.
练习册系列答案
相关题目
 作直线
作直线 交双曲线
交双曲线 于
于 、
、 两点,且
两点,且 为
为 中点.
中点.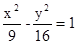 左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是
左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是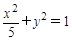 的焦点且与其对称轴成
的焦点且与其对称轴成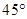 的直线与椭圆交于
的直线与椭圆交于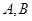 两点,
两点,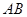 |=( ).
|=( ).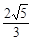

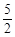
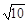
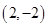 且与双曲线
且与双曲线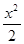 -y
-y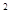 =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )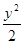 -
-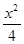 =1
=1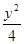 =1
=1 与双曲线
与双曲线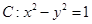 有且只有一个公共点,则
有且只有一个公共点,则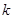 =
= 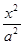 -
-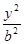 =1(
=1(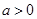 ,
,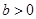 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于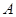 (
(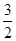 ,
,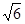 ),
),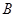 (
( ,
,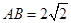 ,
,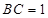 ,以
,以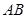 的中点
的中点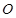 为
为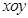 .
.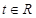 ,探究
,探究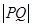 的最
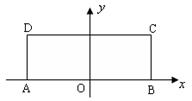
的最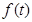 。
。
 ,
, 为坐标原点.
为坐标原点.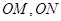 ,设
,设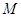 的横坐标为
的横坐标为 ,用
,用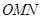 的面积,并求△
的面积,并求△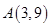 引圆
引圆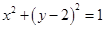 的两条切线
的两条切线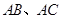 ,分别交抛物线于点
,分别交抛物线于点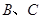 , 连接
, 连接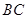 ,求直线
,求直线