题目内容
设椭圆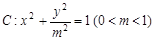 的左、右焦点分别为
的左、右焦点分别为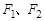 。过
。过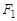 的直线
的直线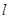 交
交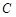 于
于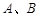 两点,且
两点,且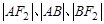 成等差数列.
成等差数列.
(1)求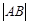 ; (2)若直线
; (2)若直线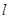 的斜率为1,求
的斜率为1,求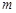 .
.
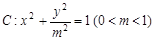 的左、右焦点分别为
的左、右焦点分别为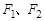 。过
。过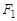 的直线
的直线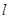 交
交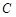 于
于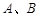 两点,且
两点,且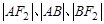 成等差数列.
成等差数列.(1)求
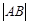 ; (2)若直线
; (2)若直线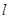 的斜率为1,求
的斜率为1,求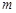 .
.(1)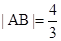 ; (2)
; (2)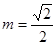
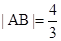 ; (2)
; (2)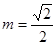
本试题主要是考查了椭圆的定义,以及直线与椭圆的位置关系的综合运用
(1)因为椭圆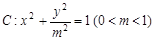 的左、右焦点分别为
的左、右焦点分别为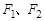 。过
。过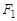 的直线
的直线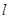 交
交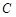 于
于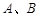 两点,且
两点,且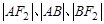 成等差数列.结合定义得到|AB|的值。
成等差数列.结合定义得到|AB|的值。
(2)联立方程组,然后结合韦达定理,得到根与系数的关系,然后直线的斜率为1,得到弦长公式的表达式,从而的得到参数m的值。
解:(1)由椭圆定义知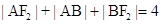
又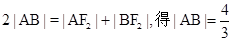 ……4分
……4分
(2)设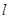 的方程为y=x+c,其中
的方程为y=x+c,其中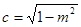 ……5分
……5分
设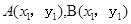
由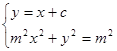
化简得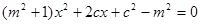
则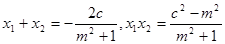 ……8分
……8分
因为直线AB的斜率为1,所以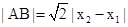
即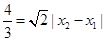 ……10分
……10分
则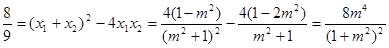
解得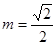 ……12分
……12分
(1)因为椭圆
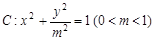 的左、右焦点分别为
的左、右焦点分别为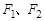 。过
。过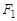 的直线
的直线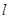 交
交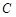 于
于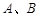 两点,且
两点,且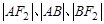 成等差数列.结合定义得到|AB|的值。
成等差数列.结合定义得到|AB|的值。(2)联立方程组,然后结合韦达定理,得到根与系数的关系,然后直线的斜率为1,得到弦长公式的表达式,从而的得到参数m的值。
解:(1)由椭圆定义知
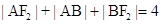
又
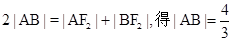 ……4分
……4分(2)设
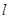 的方程为y=x+c,其中
的方程为y=x+c,其中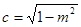 ……5分
……5分设
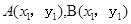
由
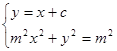
化简得
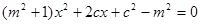
则
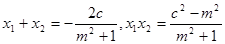 ……8分
……8分因为直线AB的斜率为1,所以
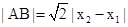
即
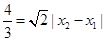 ……10分
……10分则
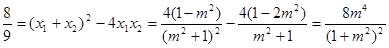
解得
 ……12分
……12分
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 :
: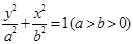 的右顶点为
的右顶点为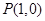 ,过
,过 .
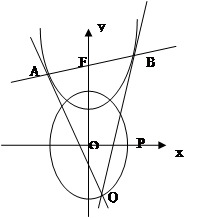
.
 :
: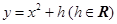 的焦点为F,过F点的直线
的焦点为F,过F点的直线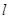 交抛物线与A、B两点,过A、B两点分别作抛物线
交抛物线与A、B两点,过A、B两点分别作抛物线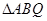 面积的最值,并求出取得最值时的抛物线
面积的最值,并求出取得最值时的抛物线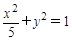 的焦点且与其对称轴成
的焦点且与其对称轴成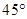 的直线与椭圆交于
的直线与椭圆交于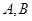 两点,
两点,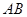 |=( ).
|=( ).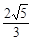

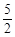
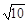
 ,
,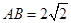 ,
,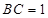 ,以
,以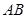 的中点
的中点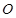 为
为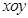 .
.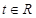 ,探究
,探究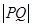 的最
的最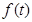 。
。
 ,
, 为坐标原点.
为坐标原点.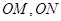 ,设
,设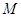 的横坐标为
的横坐标为 ,用
,用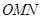 的面积,并求△
的面积,并求△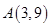 引圆
引圆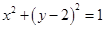 的两条切线
的两条切线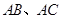 ,分别交抛物线于点
,分别交抛物线于点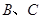 , 连接
, 连接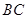 ,求直线
,求直线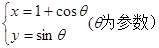 和直线
和直线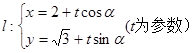
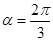 时,求圆上的点到直线
时,求圆上的点到直线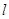 距离的最小值;
距离的最小值;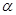 的取值范围.
的取值范围.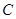 :
: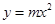 (
(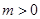 ),焦点为
),焦点为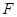 ,直线
,直线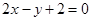 交抛物线
交抛物线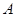 、
、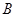 两点,
两点,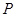 是线段
是线段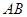 的中点,过
的中点,过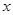 轴的垂线交抛物线
轴的垂线交抛物线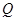 ,
,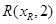 到焦点
到焦点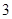 ,求此时
,求此时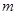 的值;
的值;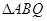 是以
是以
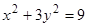 上一点P到左焦点的距离为5,则其到右焦点的距离为( )
上一点P到左焦点的距离为5,则其到右焦点的距离为( ) 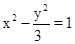 的右焦点重合,则p的值为 .
的右焦点重合,则p的值为 .