题目内容
已知抛物线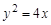 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线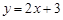 和
和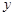 轴的距离之和的最小值
轴的距离之和的最小值
是( )
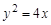 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线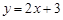 和
和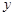 轴的距离之和的最小值
轴的距离之和的最小值是( )
A.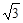 | B.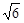 | C.2 | D.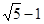 |
D
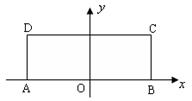
试题分析:如图由抛物线的定义知:点P到准线的距离等于点P到焦点F的距离,从而P到y轴的距离等于PF-1,过焦点F作直线y=2x+3的垂线,此时P到直线
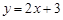 和
和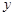 轴的距离之和为|PF|-1最小,∵F(1,0),
轴的距离之和为|PF|-1最小,∵F(1,0),有点到直线的距离公式最小值为得
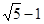 。
。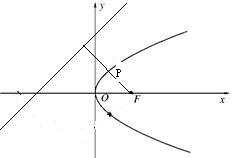
点评:解此题的关键是应用抛物线的定义对抛物线上的点到焦点的距离和到准线的距离进行灵活转化,解此题最好先画出图象,进而利用数形结合的思想解决问题.

练习册系列答案
相关题目




 作直线
作直线 交双曲线
交双曲线 于
于 、
、 两点,且
两点,且 为
为 中点.
中点. 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且
为椭圆上一点,且 ,则
,则 的面积为
的面积为


 的准线方程是( ).
的准线方程是( ).



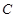 :
: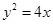 的焦点为
的焦点为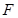 ,直线
,直线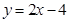 与
与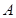 、
、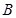 两点.则
两点.则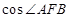 ="________."
="________." 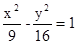 左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是
左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是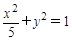 的焦点且与其对称轴成
的焦点且与其对称轴成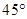 的直线与椭圆交于
的直线与椭圆交于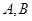 两点,
两点,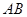 |=( ).
|=( ).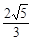

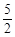
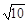
 ,
,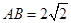 ,
,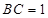 ,以
,以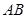 的中点
的中点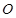 为
为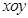 .
.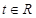 ,探究
,探究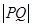 的最
的最 。
。