题目内容
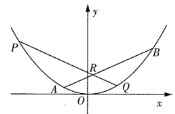
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
【答案】(1)8;(2)![]() .
.
【解析】
(1)先根据点![]() 的坐标得
的坐标得![]() 的值,然后将直线
的值,然后将直线![]() 的方程与抛物线方程联立,构建关于
的方程与抛物线方程联立,构建关于![]() 的二次方程,最后利用弦长公式求解;(2)先设出直线
的二次方程,最后利用弦长公式求解;(2)先设出直线![]() 的方程,与抛物线方程联立,构建关于
的方程,与抛物线方程联立,构建关于![]() 的二次方程,再根据点
的二次方程,再根据点![]() 的横坐标满足的条件可求得
的横坐标满足的条件可求得![]() 满足的关系式将直线
满足的关系式将直线![]() 的方程联立,可求得点
的方程联立,可求得点![]() 的横坐标,将直线
的横坐标,将直线![]() 的方程与抛物线方程联立,构建关于
的方程与抛物线方程联立,构建关于![]() 的二次方程,结合根与系数的关系、弦长公式、二次函数的最值即可求解.
的二次方程,结合根与系数的关系、弦长公式、二次函数的最值即可求解.
解:(1)![]() ,
, ![]() . 联立得
. 联立得![]() ,
,
设![]() ,则
,则![]() .
.
(2)设![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() .
.
由![]() , 联立得
, 联立得![]() ,
,
![]() , 则
, 则![]()
![]()
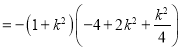
![]() .所以,当
.所以,当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
相关题目
【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: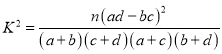 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |