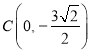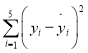题目内容
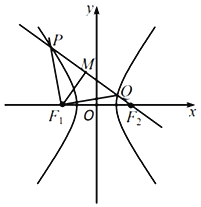
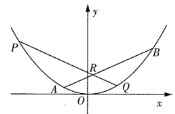
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于第一象限上的点,
上位于第一象限上的点,![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
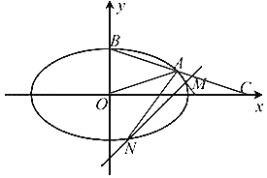
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 过椭圆
过椭圆![]() 的右焦点,且与椭圆
的右焦点,且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 在直线
在直线![]() 的同侧),若
的同侧),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() 1;(Ⅱ)x﹣y﹣2
1;(Ⅱ)x﹣y﹣2![]() 0.
0.
【解析】
(Ⅰ)运用椭圆的离心率公式和![]() 、
、![]() 、
、![]() 的关系,结合三角形的面积公式和线段的中点坐标公式,解方程可得
的关系,结合三角形的面积公式和线段的中点坐标公式,解方程可得![]() 、
、![]() ,进而得到所求椭圆方程;
,进而得到所求椭圆方程;
(Ⅱ)求得![]() 的坐标和右焦点坐标,运用等腰三角形的性质,可得线
的坐标和右焦点坐标,运用等腰三角形的性质,可得线![]() 、
、![]() 的斜率互为相反数,设直线
的斜率互为相反数,设直线![]() ,联立椭圆方程
,联立椭圆方程![]() ,运用韦达定理,求得
,运用韦达定理,求得![]() ,同理可得
,同理可得![]() ,再由直线的斜率公式,化简整理,即可得到
,再由直线的斜率公式,化简整理,即可得到![]() ,进而得到所求直线方程.
,进而得到所求直线方程.
(Ⅰ)椭圆![]() 的离心率为
的离心率为![]() ,
,
即![]() ,可得
,可得![]() ,
,![]() ,
,
由![]() ,可得
,可得 为
为![]() 的中点,
的中点,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() 1;
1;
(Ⅱ)由(Ⅰ)可得![]() ,右焦点为
,右焦点为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,直线
,直线![]() 、
、![]() 的斜率互为相反数,
的斜率互为相反数,
设直线![]() ,联立椭圆方程
,联立椭圆方程![]() ,
,
消去![]() ,可得
,可得![]() ,
,
设![]() 、
、![]() ,则
,则![]() ,所以
,所以![]() ,
,
将![]() 换为
换为![]() ,同理可得
,同理可得![]() ,
,![]() ,
,![]() ,
,
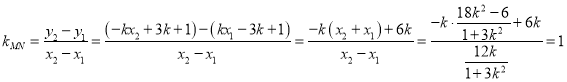 ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒闭企业所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根据上表,给出两种回归模型:
模型①:建立曲线型回归模型![]() ,求得回归方程为
,求得回归方程为![]() ;
;
模型②:建立线性回归模型![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测
,并选择拟合精度更高、更可靠的模型,预测![]() 年成立的企业中倒闭企业所占比例(结果保留整数).
年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
|
|
参考公式: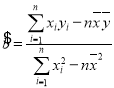 ,
,![]() ;
;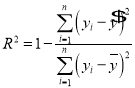 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.