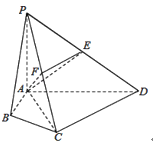
题目内容
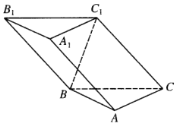
【题目】如图,在长方体ABCD﹣HKLE中,底面ABCD是边长为3的正方形,对角线AC与BD相交于点O,点F在线段AH上,且![]() ,BE与底面ABCD所成角为
,BE与底面ABCD所成角为![]() .
.
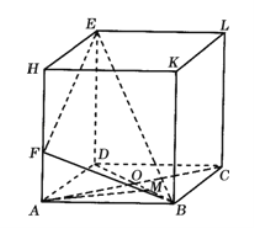
(1)求证:AC⊥BE;
(2)求二面角F﹣BE﹣D的余弦值;
(3)设点M在线段BD上,且AM//平面BEF,求DM的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可得DE⊥AC,AC⊥BD,根据线面垂直的判定可得AC⊥平面BDE,由线面垂直的性质即可得证;
(2)由DA,DC,DE两两垂直,建立空间直角坐标系D﹣xyz,求出平面BEF的一个法向量![]() 、平面BDE的一个法向量
、平面BDE的一个法向量![]() ,由
,由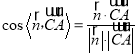 即可得解;
即可得解;
(3)设M(t,t,0),则![]() (t﹣3,t,0),由AM//平面BEF可得
(t﹣3,t,0),由AM//平面BEF可得![]() ,求得t后即可得解.
,求得t后即可得解.
(1)证明:因为在长方体ABCD﹣HKLE中, DE⊥平面ABCD,所以DE⊥AC,
因为四边形ABCD是正方形,所以AC⊥BD,
又BD∩DE=D,所以AC⊥平面BDE,
而BE平面BDE,所以AC⊥BE;
(2)因为在长方体ABCD﹣HKLE中,DA,DC,DE两两垂直,
所以建立空间直角坐标系D﹣xyz如图所示:
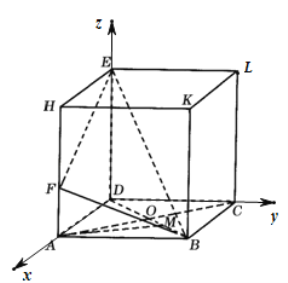
由DE⊥平面ABCD可知∠DBE为直线BE与平面ABCD所成的角,
又因为BE与平面ABCD所成角为![]() ,所以
,所以![]() ,
,
所以![]() ,由AD=3,可知
,由AD=3,可知![]() ,DE=
,DE=![]() ,
,
所以AH=3![]() ,
,
又2![]() 0,即AF
0,即AF![]() ,故AF
,故AF![]() ,
,
则A(3,0,0),F(3,0,![]() ),E(0,0,3
),E(0,0,3![]() ),B(3,3,0),C(0,3,0),
),B(3,3,0),C(0,3,0),
所以![]() (0,﹣3,
(0,﹣3,![]() ),
),![]() (3,0,﹣2
(3,0,﹣2![]() ),
),
设平面BEF的一个法向量为![]() (x,y,z),
(x,y,z),
则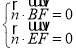 ,即
,即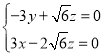 ,令
,令![]() ,则
,则![]() (4,2,
(4,2,![]() ),
),
因为AC⊥平面BDE,所以![]() 为平面BDE的一个法向量,
为平面BDE的一个法向量,![]() (3,﹣3,0),
(3,﹣3,0),
所以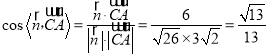 ,
,
因为二面角为锐角,所以二面角F﹣BE﹣D的余弦值为![]() ;
;
(3)因为点M是线段BD上一个动点,设M(t,t,0),则![]() (t﹣3,t,0),
(t﹣3,t,0),
因为AM//平面BEF,所以![]() ,
,
即4(t﹣3)+2t=0,解得t=2.
此时,点M坐标为(2,2,0),![]() ,符合题意.
,符合题意.

 优学名师名题系列答案
优学名师名题系列答案