题目内容
3．如果下边程序执行后输出的结果是132，那么程序中UNTIL后面的“条件”应为i＜11（或i≤10）．
分析 先根据输出的结果推出循环体执行的次数，再根据s=1×12×11=132得到程序中UNTIL后面的“条件”．
解答 解：因为输出的结果是132，即s=1×12×11，需执行2次，
则程序中UNTIL后面的“条件”应为i＜11（或i≤10）．
故答案为：i＜11（或i≤10）．
点评 本题主要考查了直到型循环语句，语句的识别问题是一个逆向性思维，一般认为学习是从算法步骤（自然语言）至程序框图，再到算法语言（程序）．如果将程序摆在我们的面前时，从识别逐个语句，整体把握，概括程序的功能，属于基础题．
练习册系列答案
相关题目
13．如图所示的程序框图，若输出的S是62，则①可以为（ ）
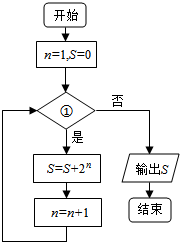
| A． | n≤3？ | B． | n≤4？ | C． | n≤5？ | D． | n≤6？ |
14．假设关于某设备的使用年限x和所支出的维修费用y（万元）有如下的统计资料：
若由资料知y对x呈线性相关关系．
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a，b；$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}，a=\overline{y}-b\overline{x}$
（3）估计使用年限为10年时，维修费用是多少？
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a，b；$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}，a=\overline{y}-b\overline{x}$
（3）估计使用年限为10年时，维修费用是多少？
18．若角α的终边经过点$（\sqrt{5}，-2）$，则sinα等于多少（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{{\sqrt{5}}}{3}$ | C． | $-\frac{2}{3}$ | D． | $-\frac{{\sqrt{5}}}{3}$ |
15．如果椭圆的两焦点为F1（-1，0）和F2（1，0），P是椭圆上的一点，且|PF1|、|F1F2|、|PF2|成等差数列，那么椭圆的方程是（ ）
| A． | $\frac{x^2}{3}+\frac{y^2}{4}$=1 | B． | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | C． | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | D． | $\frac{x^2}{16}+\frac{y^2}{12}$=1 |
在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B，经过40分钟又测得该船已行驶到点A北偏东45°+θ（其中sinθ=$\frac{\sqrt{26}}{26}$，0°＜θ＜90°）且与点A相距10$\sqrt{13}$海里的位置C．