题目内容
14.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
分析 (1)根据表格中的数据画出散点图即可;
(2)求出x与y的平均数,表示出$\sum_{i=1}^{5}{x}_{i}{y}_{i}$,$\sum_{i=1}^{5}{{x}_{i}}^{2}$,求出ξ,根据$\widehat{y}$=$\overline{y}$-ξ$\overline{x}$,计算即可得到结果;
(3)把x=10代入(2)中结果计算即可得到结果.
解答 解:(1)做出图象,如图所示: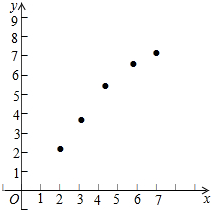 ;
;
(2)由上表得:$\overline{x}$=$\frac{2+3+4+5+6}{5}$=4,$\overline{y}$=$\frac{2.2+3.8+5.5+6.5+7}{5}$=5,
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=2×2.2+3×3.8+4×5.5+5×6.5+6×7=112.3,
$\sum_{i=1}^{5}{{x}_{i}}^{2}$=22+32+42+52+62=90,
∴ξ=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{5}{{x}_{i}}^{2}-n(\overline{x})^{2}}$=$\frac{112.3-5×4×5}{90-5×{4}^{2}}$=1.23,
则$\widehat{y}$=$\overline{y}$-ξ$\overline{x}$=1.23x+0.08;
(3)由(2)得:$\widehat{y}$=1.23x+0.08,
把x=10代入得:ξ=1.23×10+0.08=12.38,
则使用年限为10年时,维修费用是大概为12.38万元.
点评 此题考查了线性回归方程,弄清线性回归方程的意义是解本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
