题目内容
12. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向,当它行使到A的正南方向时,求该船与观测站A的距离;不改变航向继续航行,判断它是否会进入警戒水域,说明理由.
分析 (1)求得cosθ的值,进而令余弦定理求得BC,除以时间即可求得速度.
(2)建立坐标系,分别求得x2,y2,进而求得过直线B,C的直线l的斜率,求得直线l的方程.进而求得点E到直线的距离判断与7的大小关系.
解答 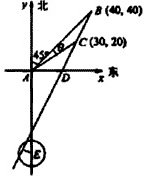 解:(1)如图,AB=40$\sqrt{2}$,AC=10$\sqrt{13}$,∠BAC=θ,sinθ=$\frac{\sqrt{26}}{26}$,
解:(1)如图,AB=40$\sqrt{2}$,AC=10$\sqrt{13}$,∠BAC=θ,sinθ=$\frac{\sqrt{26}}{26}$,
由于°<θ<90°,
所以cosθ=$\sqrt{1-(\frac{\sqrt{26}}{26})^{2}}$=$\frac{5\sqrt{26}}{26}$
由余弦定理得BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•AC•cosθ}$=10$\sqrt{5}$
所以船的行驶速度为$\frac{10\sqrt{5}}{\frac{2}{3}}$=15$\sqrt{5}$(海里/小时);
(2)如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是B(x1,y1),C(x1,y2),BC与x轴的交点为D
由题设有x1=y1=$\frac{\sqrt{2}}{2}$AB=40
x2=ACcos∠CAD=10$\sqrt{13}$cos(45°-θ)=30,
y2=ACsin∠CAD=10$\sqrt{13}$(45°-θ)=20
所以过点B、C的直线l的斜率k=$\frac{20}{10}$=2,
直线l的方程为y=2x-40
又点E(0,-55)到直线l的距离d=$\frac{|0+55-40|}{\sqrt{1+4}}$=3$\sqrt{5}$<7,
所以船会进入警戒水域.
点评 本题主要考查了解三角形问题的实际应用.建立数学模型,把实际问题转化为几何知识来解决.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目

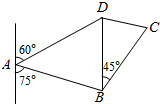 如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?
如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?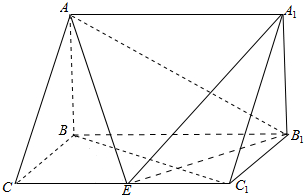 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.