题目内容
15.如果椭圆的两焦点为F1(-1,0)和F2(1,0),P是椭圆上的一点,且|PF1|、|F1F2|、|PF2|成等差数列,那么椭圆的方程是( )| A. | $\frac{x^2}{3}+\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | C. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{12}$=1 |
分析 利用已知条件结合椭圆的简单性质,椭圆的定义求解椭圆的标准方程即可.
解答 解:由|PF1|、|F1F2|、|PF2|成等差数列得|PF1|+|PF2|=2|F1F2|=4,
即2a=4,a=2,∴b2=3.
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
故选:B.
点评 本题考查椭圆的简单性质以及椭圆方程的求法,基本知识的考查.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
5.演绎推理“因为f′(x0)=0时,x0是f(x)的极值点.而对于函数f(x)=x3,f′(0)=0.所以0是函数f(x)=x3的极值点.”所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |

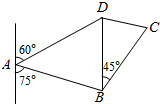 如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?
如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?