题目内容
(本小题满分12分)
已知函数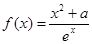
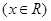 (
(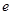 是自然对数的底数,
是自然对数的底数,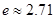 ).
).
(1)当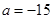 时,求
时,求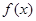 的单调区间;
的单调区间;
(2)若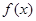 在区间
在区间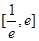 上是增函数,求实数
上是增函数,求实数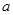 的取值范围;
的取值范围;
(3)证明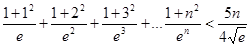 对一切
对一切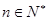 恒成立.
恒成立.
已知函数
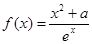
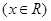 (
(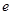 是自然对数的底数,
是自然对数的底数,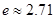 ).
).(1)当
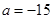 时,求
时,求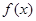 的单调区间;
的单调区间;(2)若
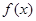 在区间
在区间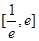 上是增函数,求实数
上是增函数,求实数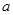 的取值范围;
的取值范围;(3)证明
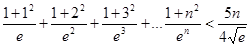 对一切
对一切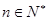 恒成立.
恒成立.(1)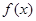 在区间
在区间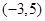 上单调递增,在区间
上单调递增,在区间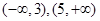 上单调递减。
上单调递减。
(2)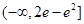 ;(3)
;(3)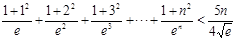 .
.
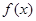 在区间
在区间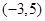 上单调递增,在区间
上单调递增,在区间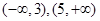 上单调递减。
上单调递减。(2)
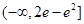 ;(3)
;(3)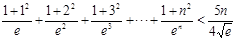 .
. 本试题主要是考查了导数在研究函数中的 运用。利用导数的符号判定函数单调性和利用单调性逆向求解参数的范围,和不等式的证明。
(1)首先求解定义域和导数,然后令导数大于零,小于零得到单调区间。
(2)因为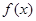 在区间
在区间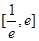 上是增函数,则说明函数在给定区间的导函数恒大于等于零,利用分离参数的思想求解参数的取值范围。
上是增函数,则说明函数在给定区间的导函数恒大于等于零,利用分离参数的思想求解参数的取值范围。
(3)利用第一问中函数的结论,令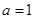 得
得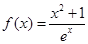 ,
,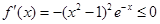 ,那么所以
,那么所以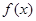 在
在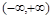 上为减函数,可得对于任意
上为减函数,可得对于任意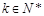 ,都有
,都有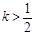 ,故有
,故有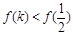
,放缩法证明不等式。
解:(1)当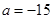 时,
时,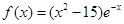 ,
,
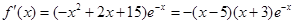
由 ,……………………………………………..4分
,……………………………………………..4分
所以,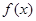 在区间
在区间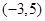 上单调递增,在区间
上单调递增,在区间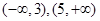 上单调递减。
上单调递减。
(2)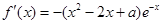 ,
,
由题意得当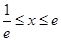 时,
时,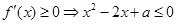 恒成立。
恒成立。
令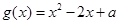 ,有
,有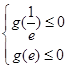 ,得
,得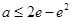 ,
,
所以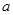 的范围是
的范围是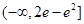 …………………………………………8分
…………………………………………8分
(3)令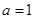 得
得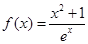 ,
,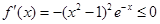 ,
,
所以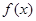 在
在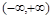 上为减函数,对于任意
上为减函数,对于任意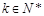 ,都有
,都有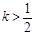 ,故有
,故有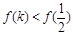
即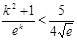
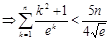
即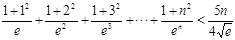 . ………12分
. ………12分
(1)首先求解定义域和导数,然后令导数大于零,小于零得到单调区间。
(2)因为
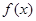 在区间
在区间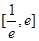 上是增函数,则说明函数在给定区间的导函数恒大于等于零,利用分离参数的思想求解参数的取值范围。
上是增函数,则说明函数在给定区间的导函数恒大于等于零,利用分离参数的思想求解参数的取值范围。(3)利用第一问中函数的结论,令
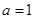 得
得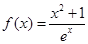 ,
,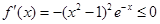 ,那么所以
,那么所以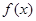 在
在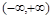 上为减函数,可得对于任意
上为减函数,可得对于任意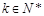 ,都有
,都有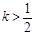 ,故有
,故有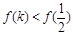
,放缩法证明不等式。
解:(1)当
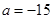 时,
时,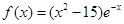 ,
,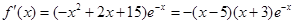
由
 ,……………………………………………..4分
,……………………………………………..4分所以,
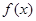 在区间
在区间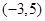 上单调递增,在区间
上单调递增,在区间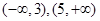 上单调递减。
上单调递减。(2)
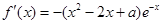 ,
,由题意得当
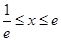 时,
时,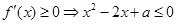 恒成立。
恒成立。令
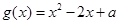 ,有
,有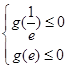 ,得
,得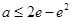 ,
,所以
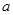 的范围是
的范围是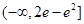 …………………………………………8分
…………………………………………8分(3)令
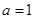 得
得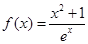 ,
,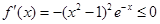 ,
,所以
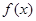 在
在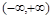 上为减函数,对于任意
上为减函数,对于任意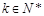 ,都有
,都有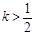 ,故有
,故有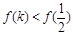
即
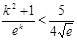
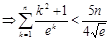
即
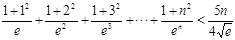 . ………12分
. ………12分
练习册系列答案
相关题目
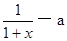 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)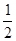
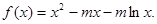
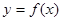 在点(1,
在点(1,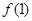 )处的切线与x轴平行.
)处的切线与x轴平行.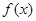 的最值;
的最值;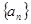 满足
满足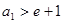 (
(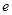 为自然对数的底数),
为自然对数的底数),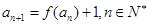 ,
,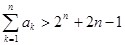 .
.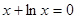 的实根为
的实根为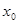 .
.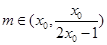 ,存在
,存在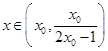 使
使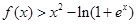 成立.
成立.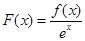 是定义在R上的函数,其中
是定义在R上的函数,其中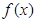 的导函数为
的导函数为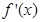 ,满足
,满足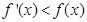 对于
对于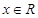 恒成立,则( )
恒成立,则( )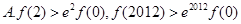


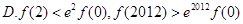
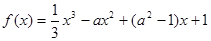 的极小值点在(0,1)内,则实数
的极小值点在(0,1)内,则实数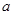 的取值范围是( )
的取值范围是( ) ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )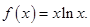
 的极值点;
的极值点;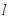 过点
过点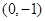 且与曲线
且与曲线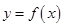 相切,求直线
相切,求直线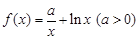 .
.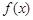 在
在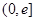 上的单调性(
上的单调性(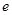 为自然对数的底);
为自然对数的底);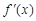 为
为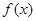 的导函数,若函数
的导函数,若函数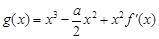 在区间
在区间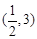 上存在极值,求实数
上存在极值,求实数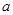 的取值范围。
的取值范围。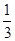 x3-(1+a)x2+4ax+24a,其中常数a>1.
x3-(1+a)x2+4ax+24a,其中常数a>1.