题目内容
已知函数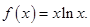
(1)求函数 的极值点;
的极值点;
(2)若直线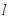 过点
过点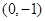 且与曲线
且与曲线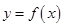 相切,求直线
相切,求直线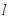 的方程;
的方程;
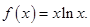
(1)求函数
 的极值点;
的极值点;(2)若直线
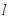 过点
过点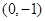 且与曲线
且与曲线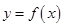 相切,求直线
相切,求直线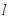 的方程;
的方程;(1)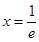 是函数
是函数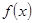 的极小值点,极大值点不存在.(2)
的极小值点,极大值点不存在.(2)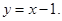
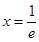 是函数
是函数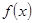 的极小值点,极大值点不存在.(2)
的极小值点,极大值点不存在.(2)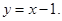
(1)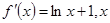 >0 …………1分
>0 …………1分
而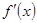 >0
>0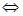 lnx+1>0
lnx+1>0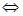
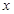 >
>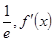 <0
<0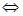
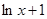 <0
<0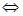 0<
0<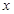 <
<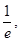 所以
所以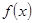 在
在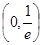 上单调递减,在
上单调递减,在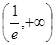 上单调递增.………………3分
上单调递增.………………3分
所以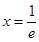 是函数
是函数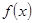 的极小值点,极大值点不存在.…………………4分
的极小值点,极大值点不存在.…………………4分
(2)设切点坐标为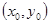 ,则
,则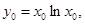 切线的斜率为
切线的斜率为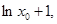
所以切线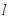 的方程为
的方程为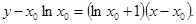 …………6分
…………6分
又切线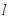 过点
过点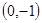 ,所以有
,所以有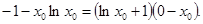
解得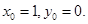 所以直线
所以直线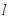 的方程为
的方程为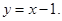 ………8分
………8分
(3)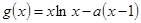 ,则
,则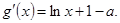
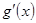 <0
<0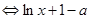 <0
<0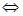 0<
0<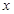 <
<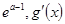 >0
>0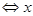 >
>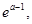 所以
所以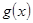 在
在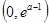 上单调递减,在
上单调递减,在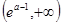 上单调递增.………………9分
上单调递增.………………9分
当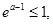 即
即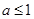 时,
时,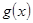 在
在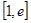 上单调递增,所以
上单调递增,所以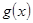 在
在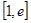 上的最小值为
上的最小值为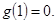 ……10分
……10分
当1<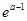 <e,即1<a<2时,
<e,即1<a<2时,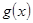 在
在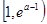 上单调递减,在
上单调递减,在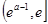 上单调递增.
上单调递增.
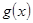 在
在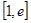 上的最小值为
上的最小值为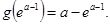 ………12分
………12分
当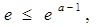 即
即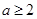 时,
时,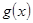 在
在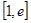 上单调递减,
上单调递减,
所以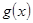 在
在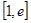 上的最小值为
上的最小值为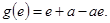 ……13分
……13分
综上,当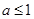 时,
时,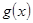 的最小值为0;当1<a<2时,
的最小值为0;当1<a<2时,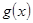 的最小值为
的最小值为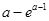 ;
;
当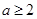 时,
时,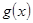 的最小值为
的最小值为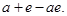 ………14分
………14分
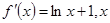 >0 …………1分
>0 …………1分而
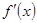 >0
>0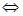 lnx+1>0
lnx+1>0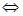
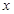 >
>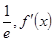 <0
<0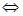
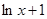 <0
<0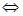 0<
0<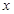 <
<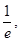 所以
所以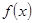 在
在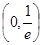 上单调递减,在
上单调递减,在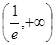 上单调递增.………………3分
上单调递增.………………3分所以
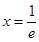 是函数
是函数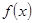 的极小值点,极大值点不存在.…………………4分
的极小值点,极大值点不存在.…………………4分(2)设切点坐标为
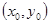 ,则
,则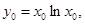 切线的斜率为
切线的斜率为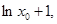
所以切线
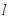 的方程为
的方程为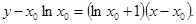 …………6分
…………6分又切线
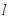 过点
过点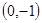 ,所以有
,所以有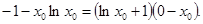
解得
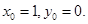 所以直线
所以直线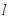 的方程为
的方程为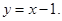 ………8分
………8分(3)
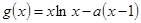 ,则
,则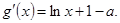
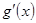 <0
<0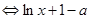 <0
<0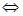 0<
0<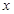 <
<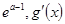 >0
>0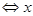 >
>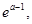 所以
所以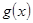 在
在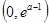 上单调递减,在
上单调递减,在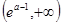 上单调递增.………………9分
上单调递增.………………9分当
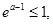 即
即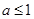 时,
时,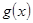 在
在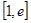 上单调递增,所以
上单调递增,所以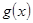 在
在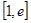 上的最小值为
上的最小值为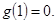 ……10分
……10分当1<
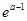 <e,即1<a<2时,
<e,即1<a<2时,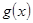 在
在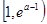 上单调递减,在
上单调递减,在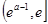 上单调递增.
上单调递增.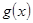 在
在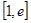 上的最小值为
上的最小值为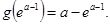 ………12分
………12分当
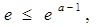 即
即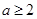 时,
时,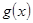 在
在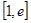 上单调递减,
上单调递减,所以
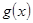 在
在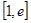 上的最小值为
上的最小值为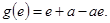 ……13分
……13分综上,当
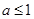 时,
时,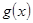 的最小值为0;当1<a<2时,
的最小值为0;当1<a<2时,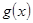 的最小值为
的最小值为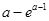 ;
;当
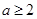 时,
时,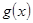 的最小值为
的最小值为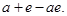 ………14分
………14分
练习册系列答案
相关题目
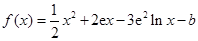 在
在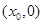 处的切线斜率为零.
处的切线斜率为零.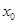 和
和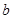 的值;
的值;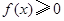 恒成立;
恒成立;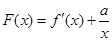 有最小值
有最小值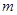 ,且
,且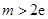 ,求实数
,求实数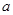 的取值范围.
的取值范围.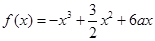 .
.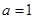 时,求
时,求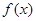 在区间
在区间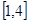 上的最值;
上的最值;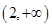 上存在单调递增区间,求
上存在单调递增区间,求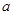 的取值范围.
的取值范围.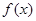 满足
满足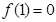 ,当
,当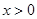 时有
时有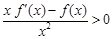 ,则不等式
,则不等式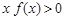 的解集为( )
的解集为( )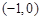
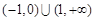
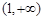
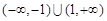
 ,
,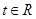 .
. 依次在
依次在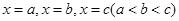 处取到极值.
处取到极值.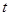 的取值范围;
的取值范围; ,求
,求 ,使对任意的
,使对任意的 ,不等式
,不等式 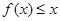 恒成立.求正整数
恒成立.求正整数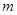 的最大值
的最大值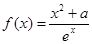
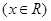 (
(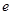 是自然对数的底数,
是自然对数的底数,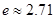 ).
).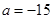 时,求
时,求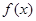 的单调区间;
的单调区间;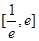 上是增函数,求实数
上是增函数,求实数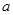 的取值范围;
的取值范围;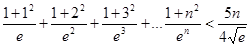 对一切
对一切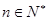 恒成立.
恒成立.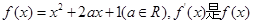 的导函数。
的导函数。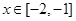 ,不等式
,不等式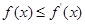 恒成立,求a的取值范围;
恒成立,求a的取值范围;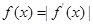 ;
;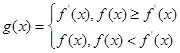 ,求
,求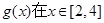 时的最小值;
时的最小值;
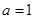 时,求函数
时,求函数 的图象在点A(0,
的图象在点A(0, )处的切线方程;
)处的切线方程;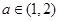 ,使
,使 当
当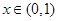 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
 若过两点
若过两点 的直线I与x轴的交点在曲线
的直线I与x轴的交点在曲线 上,求α的值。
上,求α的值。