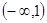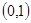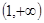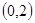题目内容
.函数f(x)=x3+ax+1在(- ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
 ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )| A. | B.1 | C. | D.-1 |
C
解:因为数f(x)=x3+ax+1在(- ,-1)上为增函数,在(-1,1)上为减函数,说明函数在x=-1处取得极大值,因此导数值为0,因此可知a=-1,进而可知f(1)为,选C
,-1)上为增函数,在(-1,1)上为减函数,说明函数在x=-1处取得极大值,因此导数值为0,因此可知a=-1,进而可知f(1)为,选C
 ,-1)上为增函数,在(-1,1)上为减函数,说明函数在x=-1处取得极大值,因此导数值为0,因此可知a=-1,进而可知f(1)为,选C
,-1)上为增函数,在(-1,1)上为减函数,说明函数在x=-1处取得极大值,因此导数值为0,因此可知a=-1,进而可知f(1)为,选C
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
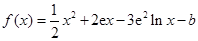 在
在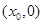 处的切线斜率为零.
处的切线斜率为零.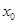 和
和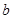 的值;
的值;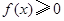 恒成立;
恒成立;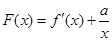 有最小值
有最小值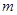 ,且
,且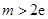 ,求实数
,求实数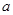 的取值范围.
的取值范围.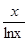 的单调递减区间是
的单调递减区间是  若函数
若函数 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。 ,
,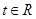 .
. 依次在
依次在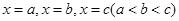 处取到极值.
处取到极值.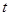 的取值范围;
的取值范围; ,求
,求 ,使对任意的
,使对任意的 ,不等式
,不等式 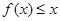 恒成立.求正整数
恒成立.求正整数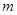 的最大值
的最大值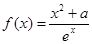
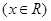 (
(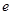 是自然对数的底数,
是自然对数的底数,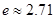 ).
).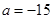 时,求
时,求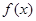 的单调区间;
的单调区间;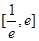 上是增函数,求实数
上是增函数,求实数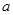 的取值范围;
的取值范围;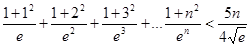 对一切
对一切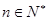 恒成立.
恒成立.
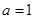 时,求函数
时,求函数 的图象在点A(0,
的图象在点A(0, )处的切线方程;
)处的切线方程;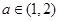 ,使
,使 当
当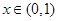 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
 轴对称;
轴对称;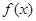 在
在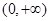 上的单调性;
上的单调性;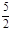 ,求此时a的值.
,求此时a的值.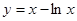 的单调减区间是 ( )
的单调减区间是 ( )