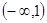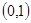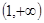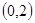题目内容
(本小题满分12分)已知函数y=f(x)在定义域(—1+∞)内满足f(o)=0,且f/(x)= 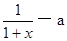 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)
(Ⅰ)求f(x)的表达式.
(Ⅱ)当a=1时,讨论f(x)的单调性
(Ⅲ)设h(x)=(ex—P)2+(x-P)2,证明:h(x)≥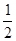
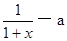 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)(Ⅰ)求f(x)的表达式.
(Ⅱ)当a=1时,讨论f(x)的单调性
(Ⅲ)设h(x)=(ex—P)2+(x-P)2,证明:h(x)≥
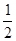
(Ⅰ)f(x)=ln(1+x)—ax.
(Ⅱ)f(x)在(-1,0)上单调增,在(0,+∞)上单调减;
(Ⅲ)h(x)=(ex-P)2+(P-x)2≥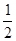 。
。
(Ⅱ)f(x)在(-1,0)上单调增,在(0,+∞)上单调减;
(Ⅲ)h(x)=(ex-P)2+(P-x)2≥
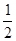 。
。本试题主要是考查了导数在研究函数中的运用。
(1)利用函数y=f(x)在定义域(—1+∞)内满足f(o)=0,且f/(x)=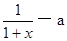 ,可以得到函数的解析式。
,可以得到函数的解析式。
(2)根据a=1,分析f(x)= ln(1+x)—x. (x>-1)
,求解导数,然后令导数大于零或者小于零得到单调区间,进而得结论。
(3)根据由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x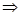 ex-x≥1 ∴(ex-x)2≥1,从而证明不等式。
ex-x≥1 ∴(ex-x)2≥1,从而证明不等式。
(Ⅰ)由f/(x)= .可得f(x)=ln(1+x)—ax+b,b为实常数.又f(0)=0
.可得f(x)=ln(1+x)—ax+b,b为实常数.又f(0)=0 b=0.
b=0.
 f(x)=ln(1+x)—ax.
f(x)=ln(1+x)—ax.
(Ⅱ)当a=1时,f(x)= ln(1+x)—x. (x>-1)
f/(x)=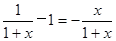 ∵x>-1
∵x>-1
由f/(x)=0 x=0 ∴当x∈(-1,0]时f/(x)≥0,此时f(x)递增
x=0 ∴当x∈(-1,0]时f/(x)≥0,此时f(x)递增
当x∈(0,+∞)时,f/(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减…………………………8分
(Ⅲ)由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x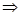 ex-x≥1 ∴(ex-x)2≥1
ex-x≥1 ∴(ex-x)2≥1
∴≤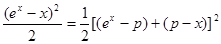 ≤(ex-P)2+(P-x)2
≤(ex-P)2+(P-x)2
即h(x)=(ex-P)2+(P-x)2≥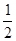 …………………………12分
…………………………12分
(1)利用函数y=f(x)在定义域(—1+∞)内满足f(o)=0,且f/(x)=
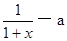 ,可以得到函数的解析式。
,可以得到函数的解析式。(2)根据a=1,分析f(x)= ln(1+x)—x. (x>-1)
,求解导数,然后令导数大于零或者小于零得到单调区间,进而得结论。
(3)根据由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x
 ex-x≥1 ∴(ex-x)2≥1,从而证明不等式。
ex-x≥1 ∴(ex-x)2≥1,从而证明不等式。(Ⅰ)由f/(x)=
 .可得f(x)=ln(1+x)—ax+b,b为实常数.又f(0)=0
.可得f(x)=ln(1+x)—ax+b,b为实常数.又f(0)=0 b=0.
b=0. f(x)=ln(1+x)—ax.
f(x)=ln(1+x)—ax.(Ⅱ)当a=1时,f(x)= ln(1+x)—x. (x>-1)
f/(x)=
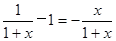 ∵x>-1
∵x>-1由f/(x)=0
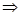 x=0 ∴当x∈(-1,0]时f/(x)≥0,此时f(x)递增
x=0 ∴当x∈(-1,0]时f/(x)≥0,此时f(x)递增当x∈(0,+∞)时,f/(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减…………………………8分
(Ⅲ)由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x
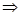 ex-x≥1 ∴(ex-x)2≥1
ex-x≥1 ∴(ex-x)2≥1∴≤
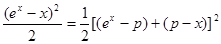 ≤(ex-P)2+(P-x)2
≤(ex-P)2+(P-x)2即h(x)=(ex-P)2+(P-x)2≥
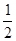 …………………………12分
…………………………12分
练习册系列答案
相关题目
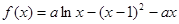 (常数
(常数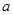
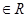 ).
).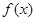 的单调区间;(5分)
的单调区间;(5分)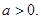 如果对于
如果对于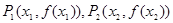
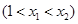 ,存在
,存在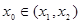 ,使得
,使得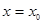 处的切线
处的切线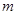 ∥
∥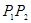 ,求证:
,求证: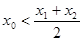 .(7分)
.(7分)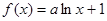
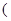
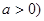 .
.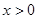 时,求证:
时,求证: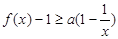 ;(4分)
;(4分)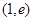 上
上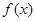
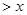 恒成立,求实数
恒成立,求实数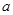 的范围。(4分)
的范围。(4分)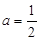 时,求证:
时,求证: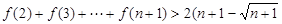 )
)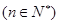 .(4分)
.(4分)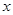 ,有
,有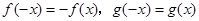 ,且
,且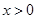 时,
时,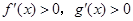 ,则
,则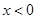 时( )
时( )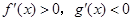
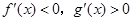
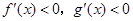
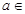 R,函数
R,函数 (x∈R).
(x∈R). 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间; 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由; 上单调递增,求
上单调递增,求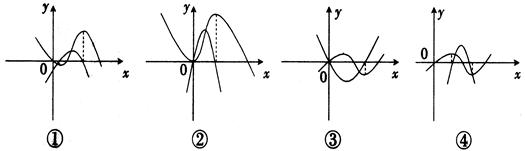
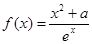
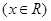 (
(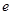 是自然对数的底数,
是自然对数的底数,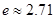 ).
).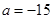 时,求
时,求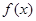 的单调区间;
的单调区间;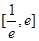 上是增函数,求实数
上是增函数,求实数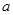 的取值范围;
的取值范围;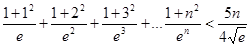 对一切
对一切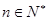 恒成立.
恒成立.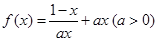 .
.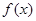 在
在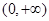 的单调性并证明;
的单调性并证明;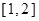 上的最小值。
上的最小值。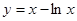 的单调减区间是 ( )
的单调减区间是 ( )